Matrita
Recomandăm citirea tuturor soluţiilor deoarece acestea sunt prezentate progresiv prin optimizări.
Înainte de a prezenta soluţiile, pentru uşurinţa înţelegerii, vom transforma enunţul aşa cum urmează. Considerăm toate fracţiile cu numitor şi numărător numere naturale cuprinse între 1 şi N inclusiv. Vom identifica o fracţie x/y prin perechea (x, y). Dorim să găsim numărul de mulţimi de perechi (x, y) cu proprietatea că nu există două elemente (x1, y1) şi (x2, y2) cu x1/y1 = x2/y2.
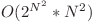
O primă soluţie care poate fi implementată pentru a verifica înţelegerea enunţului (dar care nu va obţine însă puncte) are complexitatea menţionată mai sus. Observăm că putem reprezenta o mulţime printr-o mască binară asociată, în care fiecare bit să reprezinte dacă fracţia respectivă este prezentă sau nu în mulţime. Astfel, pentru fiecare mască binară de la 1 la 2{n2}-1 putem itera prin toţi biţii săi şi, pentru a verifica dacă am obţinut o configuraţie validă, să utilizăm un hash pe numere reale.
Pentru a face trecerea de la soluţiile exponenţiale la soluţiile polinomiale vom face următoarea observaţie: dacă împărţim toate fracţiile în “clase de echivalenţă” în funcţie de fracţia ireductibilă asociată, observăm că fiecare fracţie ireductibilă contribuie în mod independent la soluţie. Astfel, prezenţa într-o mulţime a unei fracţii aparţinând unei anumite clase de echivalenţă nu influenţează în niciun fel prezenţa în aceeaşi mulţime a unei fracţii din altă clasă. Prin urmare, este suficient ca pentru fiecare fracţie ireductibilă să reţinem cardinalul clasei sale de echivalenţă. Dacă acesta este k, atunci această clasă va contribui la rezultat printr-un factor de (1 + k) (putem lua 0 numere din această clasă, sau pe oricare din cele k). Având în vedere această observaţie, răspunsul dorit va avea următoarea formă:
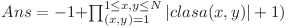
unde scăderea cu 1 este necesară întrucât mulţimea vidă nu este luată în calcul.
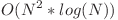 - 10 puncte
- 10 puncte
Pentru fiecare fracţie, folosim algoritmul lui Euclid pentru a o aduce la forma sa ireductibilă. Cu ajutorul unui vector de frecvenţă, putem calcula uşor cardinalele claselor de echivalenţă.
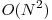 – 15-20 de puncte
– 15-20 de puncte
Observăm că putem parcurge fracţiile în ordine crescătoare după x şi în caz de egalitate dupa y pentru a stabili dacă sunt ireductibile. Astfel, dacă o fracţie nu a fost marcată, considerăm că este ireductibilă. În acest caz, parcurgem toate fracţiile de forma (k*x, k*y) şi le marcăm ca fiind reductibile. Cardinalul unei clase de echivalenţă va fi 1 + numărul de fracţii reductibile marcate pentru fracţia ireductibilă curentă.
În continuare, vom separa problema în 3 subprobleme separate: fracţiile subunitare, cele egale cu 1 şi cele supraunitare. Toate fracţiile egale cu 1 vor intra în aceeaşi clasă de echivalenţă, care are cardinalul N. Încă o observaţie este că numărul de soluţii pentru fracţiile subunitare este egal cu cel pentru fracţiile supraunitare. Astfel, dacă răspunsul pentru prima subproblema este x, răspunsul va fi:
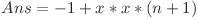
Aşadar, am redus problema la fracţiile de forma (x, y) cu x < y. Fie (x, y) o astfel de fracţie ireductibilă. Atunci, clasa sa de echivalenţă este formată din (x, y), (2x, 2y), (3x, 3y), ..., (kx, ky), unde k este cel mai mare număr natural cu proprietatea că kx, ky ≤ n (observaţie: k este chiar cardinalul clasei). Cum x < y, este suficient să spunem că ky ≤ N, adică k = [n / y], unde [a] reprezintă partea întreagă a numărului a. Prin urmare, orice fracţie ireductibilă cu numitorul y va contribui la răspuns cu un factor de (1 + [n / y]).
Notăm cu phi(n) indicatorul lui Euler pentru numărul n, care reprezintă numărul de numere naturale mai mici sau egale cu n care sunt relativ prime cu n. Numărul de fracţii ireductibile cu numitorul y va fi phi(y). Deci fiecare numitor y va contribui la răspuns cu un factor de (1 + [n/y])phi(y).
În continuare, vom considera următoarele două probleme: calculul lui phi(i), pentru fiecare i de la 1 la n şi calculul rezultatului. Următoarele complexităţi vor fi exprimate sub forma 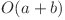 , unde a este complexitatea primei probleme, iar b a celei de-a doua.
, unde a este complexitatea primei probleme, iar b a celei de-a doua.
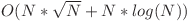 – 50 de puncte
– 50 de puncte
Pentru a calcula phi(n) vom folosi următoarea formulă:
Phi(n) = n * (1 – 1/p1) * (1 – 1/p2) * ... * (1 – 1/pd),
unde p1, p2, ..., pd sunt divizorii primi ai lui n. O soluţie care realizează calculul în 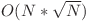 constă în descompunerea fiecărui număr de la 1 la N în factori primi în
constă în descompunerea fiecărui număr de la 1 la N în factori primi în 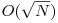 timp şi calcularea folosind formula de mai sus.
timp şi calcularea folosind formula de mai sus.
Calculul răspunsului în 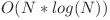 se va realiza folosind observaţiile anterioare. Astfel, pentru fiecare valoare y de la 1 la N calculăm (1 + [n/y])phi(y) folosind exponenţiere în timp logaritmic.
se va realiza folosind observaţiile anterioare. Astfel, pentru fiecare valoare y de la 1 la N calculăm (1 + [n/y])phi(y) folosind exponenţiere în timp logaritmic.
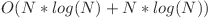 – 60 de puncte
– 60 de puncte
Complexitatea se obţine din optimizarea calculului vectorului phi. Vom folosi un algoritm similar ciurului. Utilizând ciurul obişnuit, putem determina cu uşurinţă dacă un număr este prim sau nu. În caz afirmativ, iterăm prin toţi multiplii săi şi modificăm corespunzător indicatorul lui Euler.
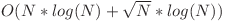 – 85 de puncte
– 85 de puncte
Acum vom optimiza calculul soluţiei. Vom demonstra că numărul de valori diferite ale lui 1 + [n/y] este de ordinul lui 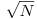 . Pentru numerele cuprinse între 1 şi
. Pentru numerele cuprinse între 1 şi 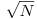 obţinem, în mod evident, maxim
obţinem, în mod evident, maxim 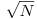 valori diferite, iar pentru numerele cuprinse între
valori diferite, iar pentru numerele cuprinse între 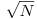 şi
şi  , [n/y] este cuprins între 1 şi
, [n/y] este cuprins între 1 şi 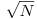 deci, va lua din nou maxim
deci, va lua din nou maxim 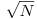 valori diferite. Astfel, putem itera prin numerele de la 1 la N şi, în loc să apelăm de fiecare dată exponenţierea logaritmică, o vom apela doar atunci când se va modifica valoarea lui 1 + [n/y].
valori diferite. Astfel, putem itera prin numerele de la 1 la N şi, în loc să apelăm de fiecare dată exponenţierea logaritmică, o vom apela doar atunci când se va modifica valoarea lui 1 + [n/y].
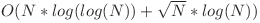 – 90 de puncte
– 90 de puncte
Pentru a obţine complexitatea N*log(log(N)) la calcularea de phi, vom ţine un vector auxiliar, prime[i], care reprezintă cel mai mic divizor prim al numărului i. Acest vector se poate calcula cu ciurul cu complexitatea amintită mai sus (iterare cu i de la 1 până la radical, iar apoi cu j de la i * i pana la N din i în i). După calculul acestui vector, vom parcurge în ordine crescătoare numerele de la 1 la N. Dacă valoarea curentă este i, avem două cazuri:
- i / prime[i] este divizibil cu prime[i], caz în care phi(i) = phi(i / prime[i]) * prime[i].
- i / prime[i] nu este divizibil cu prime[i], caz în care phi(i) = phi(i / prime[i]) * (prime[i] – 1).
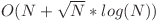 – 100 de puncte
– 100 de puncte
Ultimele 10 puncte au fost gândite mai mult în scop educativ. Pentru a le obţine este necesară calcularea vectorului phi în complexitate 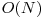 . Această soluţie implică folosirea ciurului liniar. Vom păstra vectorul auxiliar prime, cu aceeaşi semnificaţie ca mai sus. Pentru a implementa această soluţie ne vom folosi în continuare de cele două cazuri menţionate mai sus. Diferenţa este că, în loc să privim rezolvarea ca pe o dinamică unde fiecare element este calculat pe baza celor anterioare, o vom privi ca pe o dinamică în care elementul curent se extinde în cele următoare. Astfel, dacă parcurgem numerele în ordine crescătoare de la 1 la N, observăm că are sens să extindem elementul curent i doar în numerele de forma j * i, unde j este un număr prim mai mic sau egal cu prime[i]. Faptul că această soluţie este liniară reiese din faptul ca fiecare numar isi seteaza o singura data prime[i]
. Această soluţie implică folosirea ciurului liniar. Vom păstra vectorul auxiliar prime, cu aceeaşi semnificaţie ca mai sus. Pentru a implementa această soluţie ne vom folosi în continuare de cele două cazuri menţionate mai sus. Diferenţa este că, în loc să privim rezolvarea ca pe o dinamică unde fiecare element este calculat pe baza celor anterioare, o vom privi ca pe o dinamică în care elementul curent se extinde în cele următoare. Astfel, dacă parcurgem numerele în ordine crescătoare de la 1 la N, observăm că are sens să extindem elementul curent i doar în numerele de forma j * i, unde j este un număr prim mai mic sau egal cu prime[i]. Faptul că această soluţie este liniară reiese din faptul ca fiecare numar isi seteaza o singura data prime[i]
