Ecuatiile dreptei

Dreptele sunt locuri geometrice ce indeplinesc ecuatia dreptei. Cu alte cuvinte, ecuatia unei drepte reprezinta o relatie care este respectata de toate punctele aflate pe dreapta. Forma generala a ecuatiei unei drepte in sistemul xOy este

(d): a*x + b*y + c = 0

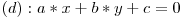
In cazul in care dreapta nu se afla in plan, fiecare punct A ( x1 , x2 , x3 ,... Xn ) (pentru n dimensiuni) de pe ea va indeplini conditiile:
$$\left\{\begin{array}{lr} x_1 = a_1\cdot x_0_1 + b_1; \ x_2 = a_2\cdot x_0_2 + b_2; \ ... \ x_n = a_n\cdot x_0_n + b_n; \end{array}\right $$

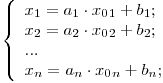
A nu se confunda cu ecuatia planului:

(d): a*x + b*y + c*z + d = 0

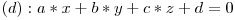
Pentru simplitate, de aici inainte ne vom referi numai la drepte in plan. De mentionat este faptul ca daca trecem pe y in partea dreapta si impartim prin -b (consideram un caz general, nu cel nefericit in care b=0), obtinem:

(d): y = \frac{(-a)}{b}*x + \frac{(-c)}{b}

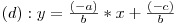
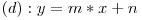(d): y = m*x + n, unde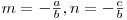 m=-\frac{a}{b}, n=-\frac{c}{b}

De asemenea, fiind date doua puncte A(x1, y1) si B(x2, y2), ecuatia dreptei determinate de ele se poate scrie

(d): \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}

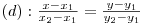
Aceasta poate sa nu ne fie de prea mare ajutor, dar facand produsul mezilor cu extremii si desfacand parantezele vom obtine 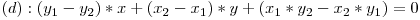(d): (y_1-y_2)*x + (x_2-x_1)*y + (x_1*y_2-x_2*y_1) = 0, de unde putem deduce foarte usor cine sunt a, b, c din scrierile precedente.

Se stie ca orice dreapta imparte planul in 2 semiplane: cel cu puncte pentru care, daca aplicam ecuatia, vom obtine o valoare strict pozitiva, si cel pentru care vom obtine o valoare strict negativa. De aceea, daca avem o dreapta data prin 2 puncte A(x1, y1) si B(x2, y2) de pe aceasta, atunci punctul C(x3, y3) va apartine dreptei AB daca si numai daca

\left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right| = 0

Panta unei drepte

Panta unei drepte se poate defini ca fiind tangenta unghiului facut de dreapta cu orizontala, mai exact cu orice dreapta paralela cu axa OX. Ea se calculeaza astfel:

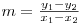m = \frac{y_1-y_2}{x_1-x_2} sau m = -\frac{a}{b}

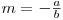
In a doua ecuatie a si b reprezinta coeficientii ecuatiei dreptei respective

(d): a*x + b*y + c = 0

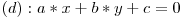
Proprietati:
• Doua drepte care au pantele egale sunt ori paralele ori confundate.
• Doua drepte care au produsul pantelor egal cu -1 sunt perpendiculare.

Distanta dintre un punct si o dreapta

Pentru a calcula distanta care ne trebuie noua vom calcula panta dreptei d1 notata cu m1. Acum vrem sa construim o dreapta d2 perpendiculara pe dreapta d1 care trece prin punctul A. Stim ca m1*m2=-1 si de aici aflam usor m2 (panta dreptei d2). In acest moment avem panta dreptei d2 si un punct care ii apartine. Avand aceste 2 informatii putem sa calculam usor ecuatia ei si punctul de intersectie cu dreapta d1 (Vezi capitolul Drepte). Distanta dintre dreapta si punct va fi egala cu distanta dintre punct si punctul de intersectie al celor 2 drepte.

De asemenea exista si o formula pt a determina distanta de la un punct la o dreapta: considerand punctul A(x0,y0) si dreapta d:ax+by+c=0, vom avea :
d(A,d) = \frac{|\mbox{a\cdot x_0+b\cdot y_0+c}|}{\mbox{\sqrt{a^2+b^2}}}

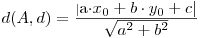
Distanta dintre un punct si un segment

Sa presupunem un punct A(x1,y1) si un segment determinat de punctele B(x2,y2) si C(x3,y3) si vrem sa aflam distanta dintre punct si segment.

D=min(dist(A,B),dist(A,C)) in cazul in care perpendiculara din punctul A pe dreapta BC nu cade in interiorul segmentului BC, altfel distanta va fi egala cu distanta dintre punctul A si dreapta BC, lucru care l-am tratat mai sus.