Revizia anterioară Revizia următoare
Coduri Gray
(Categoria Matematica, autor Cosmin Negruseri)
Introducere
Acest articol prezinta notiunea de Cod Gray si unele aplicatii ale lui in probleme de la concursurile de programare.
Un cod Gray de ordin 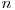 este un sir care contine toate numerele de la
este un sir care contine toate numerele de la  la
la 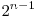 , astfel ca oricare doua numere consecutive din sir difera in reprezentarea binara prin exact un bit. Pentru
, astfel ca oricare doua numere consecutive din sir difera in reprezentarea binara prin exact un bit. Pentru 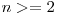 exista mai multe coduri Gray distincte. Un cod mai des intalnit, numit in engleza binary reflected Gray code (in continuare cand vom vorbi despre codul Gray ne vom referi de fapt la acest cod). Modul de constructie al acestui cod este unul intuitiv: la fiecare pas adaugam numarul adaugat anterior, caruia ii modificam cel mai putin semnificativ bit, astfel ca numarul obtinut sa nu mai fi fost adaugat inainte la sir. De exemplu, daca ordinul este doi si avem la inceput numarul
exista mai multe coduri Gray distincte. Un cod mai des intalnit, numit in engleza binary reflected Gray code (in continuare cand vom vorbi despre codul Gray ne vom referi de fapt la acest cod). Modul de constructie al acestui cod este unul intuitiv: la fiecare pas adaugam numarul adaugat anterior, caruia ii modificam cel mai putin semnificativ bit, astfel ca numarul obtinut sa nu mai fi fost adaugat inainte la sir. De exemplu, daca ordinul este doi si avem la inceput numarul  in sir, vom adauga
in sir, vom adauga  , apoi
, apoi 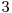 , iar apoi
, iar apoi 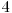 .
.
In acest articol vom nota acest cod cu 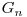 . O alta metoda de constructie care obtine acelasi cod Gray este de a determina mai intai pe
. O alta metoda de constructie care obtine acelasi cod Gray este de a determina mai intai pe 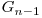 , apoi daca notam cu
, apoi daca notam cu 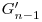 sirul
sirul 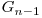 inversat, atunci obtinem pe
inversat, atunci obtinem pe 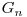 daca punem cate un bit de
daca punem cate un bit de  in fata fiecarui numar din
in fata fiecarui numar din 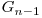 , iar acestea sunt urmate de numerele din
, iar acestea sunt urmate de numerele din 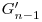 carora le adaugam cate un bit de
carora le adaugam cate un bit de  ca bit semnificativ ( pe scurt
ca bit semnificativ ( pe scurt 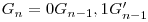 (1) ). Observam ca acest cod este unul circular, adica ultimul numar si primul numar din cod difera prin exact un bit. Observam de asemenea ca fiecare cod de ordin
(1) ). Observam ca acest cod este unul circular, adica ultimul numar si primul numar din cod difera prin exact un bit. Observam de asemenea ca fiecare cod de ordin 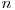 il contine pe cel de
il contine pe cel de 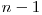 ca prefix, deci am putea nota prin
ca prefix, deci am putea nota prin 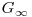 sirul numerelor naturale in care orice doua numere consecutive difera in reprezentarea binara prin exact un bit si pentru care sirul primelor
sirul numerelor naturale in care orice doua numere consecutive difera in reprezentarea binara prin exact un bit si pentru care sirul primelor 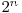 elemente coincide cu
elemente coincide cu 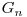 , oricare ar fi acest
, oricare ar fi acest 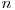 un numar natural.
un numar natural.
Fie 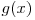 al
al  -lea numar din
-lea numar din 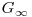 (prin
(prin 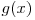 notam codul Gray al numarului
notam codul Gray al numarului  ) si
) si 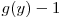 la ce pozitie apare numarul
la ce pozitie apare numarul 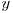 in sirul
in sirul 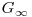 . Ne punem problema calcularii eficiente a celor doua functii. Se poate demonstra prin inductie ca daca avem un numar
. Ne punem problema calcularii eficiente a celor doua functii. Se poate demonstra prin inductie ca daca avem un numar  cu reprezentarea binara
cu reprezentarea binara 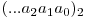 si codul lui Gray, cu reprezentarea binara
si codul lui Gray, cu reprezentarea binara 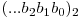 , atunci avem
, atunci avem 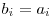 ^
^ 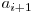 (2). De exemplu, daca avem numarul
(2). De exemplu, daca avem numarul 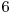 cu reprezentarea binara
cu reprezentarea binara 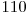 , atunci
, atunci 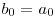 ^
^ 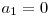 ^
^ 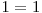 ,
, 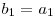 ^
^ 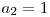 ^
^ 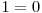 ,
, 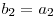 ^
^ 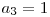 ^
^ 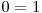 , deci
, deci 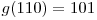 . Din aceasta relatie tragem concluzia ca
. Din aceasta relatie tragem concluzia ca 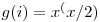 (unde prin / am notat impartire intreaga). Din (2) obtinem ca
(unde prin / am notat impartire intreaga). Din (2) obtinem ca 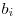 ^
^ 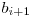 ^
^ 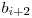 ^
^ 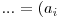 ^
^ 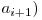 ^
^ 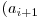 ^
^ 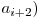 ^
^ 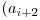 ^
^ 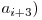 ^
^ 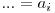 . Aceasta suma este finita deoarece vom avea un
. Aceasta suma este finita deoarece vom avea un 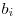 egal cu
egal cu  si un
si un 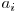 egal cu
egal cu  , daca
, daca 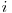 este indeajuns de mare. Astfel
este indeajuns de mare. Astfel 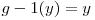 ^
^ 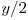 ^
^ 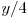 ^
^ 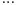
Din cele de mai sus obtinem urmatoarele metode:
int binToGray(int x) {
return x ^ (x >> 1);
}int grayToBin(int y) {
int ret = 0;
while (y > 0) {
ret ^= y;
y >>= 1;
}
return ret;
}Sa vedem mai departe cateva probleme:
Problema 1: Turnurile din Hanoi
Avem trei tije si 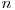 discuri de dimensiuni diferite plasate in ordinea descrescatoare a dimensiunilor pe prima tija. Se doreste mutarea tuturor discurilor pe cea de a doua tija, singurul tip de miscare posibila fiind mutarea unui disc de pe o tija pe alta, cu conditia ca pe tija destinatie discul din varf (daca exista un asemenea disc) sa fie mai mare decat discul pe care il mutam acum.
discuri de dimensiuni diferite plasate in ordinea descrescatoare a dimensiunilor pe prima tija. Se doreste mutarea tuturor discurilor pe cea de a doua tija, singurul tip de miscare posibila fiind mutarea unui disc de pe o tija pe alta, cu conditia ca pe tija destinatie discul din varf (daca exista un asemenea disc) sa fie mai mare decat discul pe care il mutam acum.
Rezolvare:
Aceasta este o problema clasica in predarea recursivitatii, dar ea are o solutie care se foloseste de codul Gray. Urmarim pas cu pas ce bit se schimba de la numerele consecutive ale lui 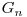 , acest bit corespunde discului pe care il vom muta (cel mai putin semnificativ bit corespunde celui mai mic disc, iar cel mai semnificativ bit corespunde celui mai mare disc). Problema este ca stim ce disc sa mutam, dar nu stim pe ce tija. Dar exista o regula simpla care ne poate ajuta: un disc nu trebuie plasat pe alt disc cu aceeasi paritate. Aceasta strategie rezolva si ea in numar minim de pasi problema, acest numar fiind
, acest bit corespunde discului pe care il vom muta (cel mai putin semnificativ bit corespunde celui mai mic disc, iar cel mai semnificativ bit corespunde celui mai mare disc). Problema este ca stim ce disc sa mutam, dar nu stim pe ce tija. Dar exista o regula simpla care ne poate ajuta: un disc nu trebuie plasat pe alt disc cu aceeasi paritate. Aceasta strategie rezolva si ea in numar minim de pasi problema, acest numar fiind 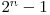 .
.
Problema 2:
Un bec este conectat la 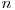 intrerupatoare. Fiecarui astfel de intrerupator ii poate fi schimbata starea prin apasare. Problema este ca nu stim starea lor initiala. Se cere sa se determine o strategie care ar face numar minim de apasari in cazul cel mai rau, pentru a aprinde becul.
intrerupatoare. Fiecarui astfel de intrerupator ii poate fi schimbata starea prin apasare. Problema este ca nu stim starea lor initiala. Se cere sa se determine o strategie care ar face numar minim de apasari in cazul cel mai rau, pentru a aprinde becul.
Rezolvare
Pentru a fi siguri ca aprindem becul trebuie in cel mai rau caz sa trecem prin toate configuratiile apasat/ne-apasat ale intrerupatoarelor. Pentru a schimba starea curenta trebuie sa apasam cel putin un buton, deci in cazul cel mai defavorabil va trebui sa facem cel putin 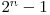 apasari. Codul Gray ne da o posibilitate de a trece prin toate configuratiile trecand de la una la alta prin o apasare de buton, rezolvandu-ne problema.
apasari. Codul Gray ne da o posibilitate de a trece prin toate configuratiile trecand de la una la alta prin o apasare de buton, rezolvandu-ne problema.
Problema 3: Matrix ( acm.sgu.ru - 249)
Trebuie sa aranjati numerele de la  la
la 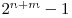 intr-o matrice cu
intr-o matrice cu 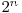 randuri si
randuri si 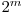 coloane. De asemenea, numerele care sunt situate in celule adiacente pe verticala sau orizontala trebuie sa difere prin exact un bit in reprezentarea lor binara. Matricea este ciclica, adica pentru fiecare rand celula cea mai din stanga se considera invecinata cu cea mai din dreapta, de asemenea pentru fiecare coloana celula cea mai de sus se considera invecinata cu celula cea mai de jos. La intrare se dau numerele
coloane. De asemenea, numerele care sunt situate in celule adiacente pe verticala sau orizontala trebuie sa difere prin exact un bit in reprezentarea lor binara. Matricea este ciclica, adica pentru fiecare rand celula cea mai din stanga se considera invecinata cu cea mai din dreapta, de asemenea pentru fiecare coloana celula cea mai de sus se considera invecinata cu celula cea mai de jos. La intrare se dau numerele 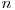 si
si 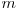 (
(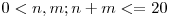 ). Trebuie sa afisati o asemenea matrice. De exemplu daca
). Trebuie sa afisati o asemenea matrice. De exemplu daca 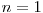 si
si 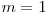 o matrice ar fi
o matrice ar fi
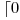
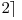
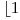
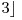 .
.
Rezolvare:
O prima metoda ar fi de determinare a codului 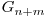 , iar apoi de a-l scrie serpuit in matrice, adica in liniile de index par de la stanga la dreapta, iar in liniile de index impar de la dreapta la stanga.
, iar apoi de a-l scrie serpuit in matrice, adica in liniile de index par de la stanga la dreapta, iar in liniile de index impar de la dreapta la stanga.
De exemplu, daca 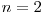 si
si 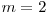 avem:
avem:
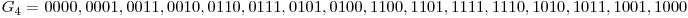
| 0000 | 0001 | 0011 | 0010 |
| 0100 | 0101 | 0111 | 0110 |
| 1100 | 1101 | 1111 | 1110 |
| 1000 | 1001 | 1011 | 1010 |
Alta modalitate de rezolvare care ne da de fapt aceeasi matrice este urmatoarea: Intregul din celula 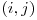 a matricei va fi in reprezentarea binara rezultatul concatenarii reprezentarii binare a intregului de index
a matricei va fi in reprezentarea binara rezultatul concatenarii reprezentarii binare a intregului de index 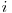 din codul
din codul 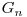 cu reprezentarea binara a intregului de index
cu reprezentarea binara a intregului de index 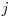 din codul
din codul 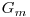 .
.
De exemplu, daca avem 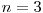 si
si 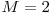 :
:
| - | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 000 | 00000 | 00001 | 00011 | 00010 |
| 001 | 00100 | 00101 | 00111 | 00110 |
| 011 | 01100 | 01101 | 01111 | 01110 |
| 010 | 01000 | 01001 | 01011 | 01010 |
| 110 | 11000 | 11001 | 11011 | 11010 |
| 111 | 11100 | 11101 | 11111 | 11110 |
| 101 | 10100 | 10101 | 10111 | 10111 |
| 100 | 10000 | 10001 | 10011 | 10010 |
Este evident ca orice doua numere din matrice vor fi diferite, orice doua numere adiacente in matrice sunt diferite in reprezentarea binara prin exact un bit. In concurs limita de timp era foarte stransa si trebuia folosita functia prezentata anterior. Deci pe linia 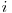 coloana
coloana 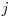 a matricei scriem numarul <code>(binToGray(i) << M) | binToGray(j)</code>.
a matricei scriem numarul <code>(binToGray(i) << M) | binToGray(j)</code>.
Problema 4: Divizori
Vom considera un numar natural  . In sirul
. In sirul 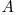 vom aseza toti divizorii lui
vom aseza toti divizorii lui 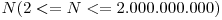 . Se cere sa se permute elementele sirului
. Se cere sa se permute elementele sirului 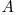 astfel incat pentru oricare doua elemente consecutive
astfel incat pentru oricare doua elemente consecutive ![A[i] A[i]](http://www.infoarena.ro/static/images/latex/8a6b5ab46e06fa60418f7c34e624b076_3.5pt.gif) si
si ![A[i+1] A[i+1]](http://www.infoarena.ro/static/images/latex/7c32aab82d95eb6cfacf9559b3b1f14f_3.5pt.gif) sa avem fie
sa avem fie ![A[i]=A[i+1]*p A[i]=A[i+1]*p](http://www.infoarena.ro/static/images/latex/95ade66258b2de95f22fb328f45c8349_3.5pt.gif) , fie
, fie ![A[i+1]=A[i]*p A[i+1]=A[i]*p](http://www.infoarena.ro/static/images/latex/8349c31601a98b44011e5add63b3026e_3.5pt.gif) , unde
, unde 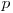 este un numar prim oarecare. Valoarea
este un numar prim oarecare. Valoarea 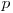 poate diferi de la o pereche de elemente la alta. De exemplu pentru
poate diferi de la o pereche de elemente la alta. De exemplu pentru 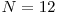 o posibila solutie ar fi
o posibila solutie ar fi 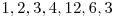 .
.
Rezolvare
Numarul  are maxim
are maxim 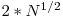 divizori. Daca descompunem numarul
divizori. Daca descompunem numarul  in factori primi atunci il vom putea scrie sub forma
in factori primi atunci il vom putea scrie sub forma 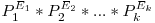 , unde
, unde 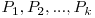 sunt numere prime si
sunt numere prime si 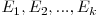 numere naturale mai mari ca zero. Un divizor al lui N va fi reprezentat printr-un vector de exponenti
numere naturale mai mari ca zero. Un divizor al lui N va fi reprezentat printr-un vector de exponenti 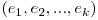 unde
unde 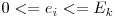 . Prin urmare, problema noastra poate fi usor redusa la urmatoarea cerinta: ordonati toti vectorii
. Prin urmare, problema noastra poate fi usor redusa la urmatoarea cerinta: ordonati toti vectorii 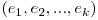 unde
unde 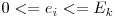 , intr-un sir cu proprietatea ca diferenta intre doi vectori consecutivi se realizeaza la o singura pozitie a vectorilor si cele doua elemente ale vectorilor de pe pozitia respectiva difera prin o unitate.
, intr-un sir cu proprietatea ca diferenta intre doi vectori consecutivi se realizeaza la o singura pozitie a vectorilor si cele doua elemente ale vectorilor de pe pozitia respectiva difera prin o unitate.
Exemplul din enuntul problemei se poate reprezenta astfel:
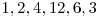
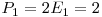

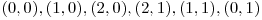
Aceasta problema este o generalizare a determinarii codului Gray si poate fi rezolvata generalizand metoda expusa mai sus. Presupunem ca stim sa generam o solutie pentru 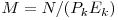 (o solutie pentru un numar cu
(o solutie pentru un numar cu 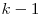 factori primi). Sa vedem cum generam o solutie pentru
factori primi). Sa vedem cum generam o solutie pentru  . Fie
. Fie 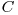 vectorul solutie pentru
vectorul solutie pentru 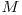 si
si 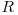 vectorul
vectorul 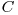 inversat (primul element al lui
inversat (primul element al lui 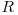 este ultimul al lui
este ultimul al lui 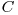 , etc.). O solutie pentru
, etc.). O solutie pentru  poate fi obtinuta in urmatoarea forma:
poate fi obtinuta in urmatoarea forma:
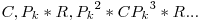
Astfel am concatenat 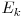 coduri pentru
coduri pentru 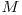 , inmultind cu
, inmultind cu 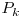 si pe fiecare pozitie impara am pus secventa inversata pentru
si pe fiecare pozitie impara am pus secventa inversata pentru 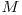 . Am facut aceasta pentru ca cele doua capete ce vor ajunge in codul final consecutive sa difere numai prin
. Am facut aceasta pentru ca cele doua capete ce vor ajunge in codul final consecutive sa difere numai prin 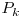 .
.
Exemplu: 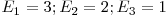
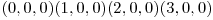
Solutia pentru un factor prim.
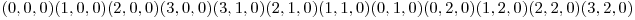
Solutia pentru doi factori primi.
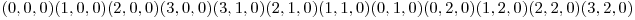
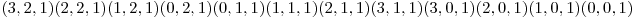
Solutia pentru cei trei factori primi.
Complexitatea finala a solutiei este 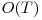 unde
unde 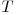 reprezinta numarul de divizori ai lui
reprezinta numarul de divizori ai lui  .
.
Problema 5: Sortnet (Mihai Patrascu, lot 2002)
O retea completa de sortare este o retea de sortare cu  fire de adancime
fire de adancime 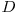 ce are
ce are 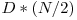 comparatori. Amintim principiul
comparatori. Amintim principiul 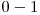 care spune ca o retea de sortare sorteaza orice
care spune ca o retea de sortare sorteaza orice  numere daca aceasta sorteaza orice secventa de
numere daca aceasta sorteaza orice secventa de  numere
numere  sau
sau  . Problema noastra cere cate astfel de secvente de
. Problema noastra cere cate astfel de secvente de  si
si  nu sunt sortate corect.
nu sunt sortate corect.
Rezolvarea lui Mihai Patrascu
Observam ca dupa primul strat de comparatori sunt exact 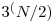 rezultate posibile, pentru ca intrarile trecute printr-un comparator se transforma astfel
rezultate posibile, pentru ca intrarile trecute printr-un comparator se transforma astfel 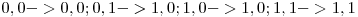 . Pentru a testa fiecare astfel de rezultat daca e sortat sau nu de urmatoarele
. Pentru a testa fiecare astfel de rezultat daca e sortat sau nu de urmatoarele 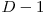 straturi, nu vor trebui simulate toate in complexitate
straturi, nu vor trebui simulate toate in complexitate 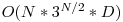 . Prin generarea secventelor conform codului Gray in baza 3 putem doar sa urmarim modificarea rezultatului pentru doua rezultate succesive in
. Prin generarea secventelor conform codului Gray in baza 3 putem doar sa urmarim modificarea rezultatului pentru doua rezultate succesive in 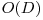 . Un numar in baza trei il transformam in unul in baza doi cu numar dublu de cifre, astfel
. Un numar in baza trei il transformam in unul in baza doi cu numar dublu de cifre, astfel  trece in
trece in 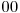 ,
,  trece in
trece in 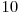 si
si 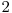 trece in
trece in 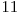 , acest cod reprezentand un rezultat posibil dupa evaluarea unei secvente binare de catre primul strat al retelei. Modificarea unei cifre in baza trei conform codului Gray generalizat pentru numere in aceasta baza, duce la modificarea unei cifre in codul binar a unui bit. Urmarirea modificarilor facute de acest bit schimbat in evaluarile facute de reteaua de sortare o putem face in complexitate
, acest cod reprezentand un rezultat posibil dupa evaluarea unei secvente binare de catre primul strat al retelei. Modificarea unei cifre in baza trei conform codului Gray generalizat pentru numere in aceasta baza, duce la modificarea unei cifre in codul binar a unui bit. Urmarirea modificarilor facute de acest bit schimbat in evaluarile facute de reteaua de sortare o putem face in complexitate 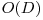 . Astfel complexitatea finala este
. Astfel complexitatea finala este  .
.
Mentionam ca problema este pe site-ul InfoArena (Sortnet) si acolo o rezolvare 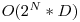 intra in timp, dar si pentru aceasta trebuie sa folosim codul Gray si sa urmarim modificarile date de schimbarea unui bit in evaluare.
intra in timp, dar si pentru aceasta trebuie sa folosim codul Gray si sa urmarim modificarile date de schimbarea unui bit in evaluare.
Dam mai jos rezolvarea eleganta si usor de inteles a lui Mircea Pasoi:
#include <stdio.h>
#define MAX_N 20
#define MAX_M 33
#define MAX_C 59049
#define FIN "sortnet.in"
#define FOUT "sortnet.out"
#define GRAY(x) ((x) ^ ((x) >> 1))
#define BIT(a, b) (((a) & (1 << (b))) > 0)
#define MIN(a, b) ((a) < (b) ? (a) : (b))
#define MAX(a, b) ((a) > (b) ? (a) : (b))
#define SORTED(x) (((x) & ((x)+1)) == 0)
#define FOR(i, a, b) for (i = (a); i < (b); i++)
int N, M, G[MAX_M][MAX_N], V[MAX_M], V2[MAX_M], Res;
int works(int n, int a)
{
int i, b, t;
V2[0] = n;
FOR (i, 0, M)
{
b = G[i][a];
if ((BIT(V[i], MAX(a, b)) && !BIT(V[i], MIN(a, b))) ||
(BIT(V2[i], MAX(a, b)) && !BIT(V2[i], MIN(a, b))))
a = b;
V[i] = V2[i];
V2[i+1] = V[i+1]^(1<<a);
}
V[M] = V2[M];
return SORTED(V[M]);
}
int main(void)
{
int i, j, k, a, b, bit;
freopen(FIN, "r", stdin);
freopen(FOUT, "w", stdout);
scanf("%d %d\n", &N, &M);
FOR (i, 0, M) FOR (j, 0, N/2)
{
scanf("<%d,%d> ", &a, &b);
a--; b--;
G[i][a] = b; G[i][b] = a;
}
Res = 1;
FOR (i, 1, (1<<N))
{
k = GRAY(i) ^ GRAY(i-1);
for (bit = 0; (1<<bit) < k; bit++);
Res += works(GRAY(i), bit);
}
printf("%d\n", Res);
return 0;
}Bibliografie
- [1] D.E.Knuth TAOC Prefascicle 2A
- [2] W.H. Press et. all. Numerical Recipies in C, Cambridge University Press
- [3] http://en.wikipedia.org/wiki/Gray_code
