Coduri Gray

(Categoria Matematica, autor Cosmin Negruseri)

Introducere

Acest articol prezinta notiunea de Cod Gray si unele aplicatii ale lui in probleme de la concursurile de programare.
Un cod Gray de ordin 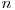este un sir care contine toate numerele de la la 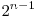, astfel ca oricare doua numere consecutive din sir difera in reprezentarea binara prin exact un bit. Pentru 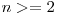exista mai multe coduri Gray distincte. Un cod mai des intalnit, numit in engleza binary reflected Gray code (in continuare cand vom vorbi despre codul Gray ne vom referi de fapt la acest cod). Modul de constructie al acestui cod este unul intuitiv: la fiecare pas adaugam numarul adaugat anterior, caruia ii modificam cel mai putin semnificativ bit, astfel ca numarul obtinut sa nu mai fi fost adaugat inainte la şir. De exemplu, dacă ordinul este doi si avem la inceput numarul in sir, vom adauga , apoi 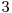, iar apoi .
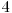In acest articol vom nota acest cod cu 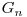. O alta metoda de constructie care obtine acelasi cod Gray este de a determina mai intai pe 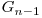, apoi daca notam cu 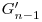sirul 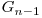inversat, atunci obtinem pe 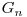daca punem cate un bit de in fata fiecarui numar din 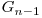, iar acestea sunt urmate de numerele din 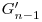carora le adaugam cate un bit de ca bit semnificativ ( pe scurt 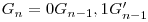(1) ). Observam ca acest cod este unul circular, adica ultimul numar si primul numar din cod difera prin exact un bit. Observam de asemenea ca fiecare cod de ordin 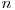il contine pe cel de 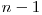ca prefix, deci am putea nota prin 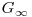sirul numerelor naturale in care orice doua numere consecutive difera in reprezentarea binara prin exact un bit si pentru care sirul primelor 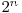elemente coincide cu 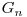, oricare ar fi acest 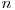un numar natural.
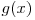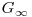Fie al -lea numar din (prin 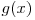notam codul Gray al numarului ) si 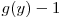la ce pozitie apare numarul 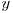in sirul 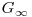. Ne punem problema calcularii eficiente a celor doua functii. Se poate demonstra prin inductie ca daca avem un numar cu reprezentarea binara 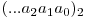si codul lui Gray, cu reprezentarea binara 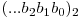, atunci avem 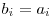^ 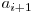(2). De exemplu, daca avem numarul 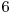cu reprezentarea binara 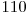, atunci 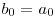^ ^ 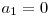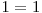, 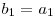^ ^ 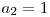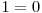, 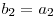^ ^ 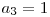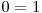, deci 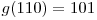. Din aceasta relatie tragem concluzia ca 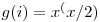(unde prin / am notat impartire intreaga). Din (2) obtinem ca 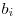^ ^ 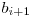^ ^ 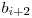^ ^ 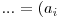^ ^ 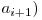^ 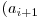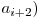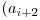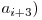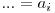. Aceasta suma este finita deoarece vom avea un 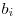egal cu si un 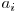egal cu , daca 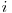este indeajuns de mare. Astfel ^ ^ ^
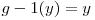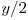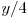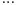
Din cele de mai sus obtinem urmatoarele metode:

int binToGray(int x) {
     return x ^ (x >> 1);
}

int  grayToBin(int y) {
     int ret = 0;
    while (y > 0) {
        ret ^= y;
        y >>= 1;
     }
     return ret;     
}

Sa vedem mai departe cateva probleme: