Cautari ortogonale: Structuri de date si aplicatii

(Categoria Structuri de date, autor Cosmin Negruseri)

Introducere

In acest articol voi discuta despre cateva structuri de date folositoare pentru probleme de geometrie, in special pentru probleme ortogonale. Problema de baza ce va fi rezolvata suna in felul urmator: avem n puncte in plan si pentru un anumit dreptunghi ne intereseaza numarul de puncte din acel dreptunghi, sau diverse alte operatii pentru punctele din interiorul sau, cum ar fi suma cheilor punctelor, minimul sau maximul cheilor (daca punctele au asociate cate o cheie). Folosind arbori de intervale putem rezolva aceasta problema, dar vreau sa exemplific ce alte variante mai avem si avantajele lor, precum si aplicatii practice pentru cautarea pe domenii ortogonale. In general, abordarile prezentate mai jos se pot extinde de la cazul unidimensional sau bidimensional, cu usurinta, la cazuri N-dimensionale.
Pentru a intelege cat mai bine ideile si structurile de date prezentate mai departe recomand citirea articolelor [1] si [2].
Structurile prezentate sunt in general statice, adica formam intai structura si apoi rezolvam problema. Structurile de date se pot modifica pentru a suporta inserari si stergeri de puncte, devenind dinamice, dar astfel implementarea se complica. Pentru a simula dinamismul putem insera toate datele de la inceput si sa mai avem un camp boolean in care marcam cu true daca data a fost logic inserata si cu false daca data din nodul respectiv nu a fost inca logic inserata. Aceasta pastreaza complexitatea operatiilor pe structura si ne ajuta in echilibrarea structurilor pentru o eficienta buna a operatiilor.

QuadTree

QuadTree este o structura care organizeaza informatii pentru date multidimensionale, fiind folosita in cartografie, procesarea imaginilor, grafica pe calculator etc. Structura este un arbore ce reprezinta o zona din spatiul N-dimensional (in cazul in care suntem noi interesati, N=2), fiecare nod al arborelui pastreaza o informatie pentru o zona din spatiu, iar nodul are 2^N fii care reprezinta fiecare o zona de 2^N ori mai mica decat zona parintelui. Zonele fiilor sunt disjuncte, iar reuniunea lor formeaza zona parintelui.

Pentru un QuadTree radacina reprezinta un patrat, iar fii reprezinta cele patru patrate disjuncte si congruente in care se poate imparti patratul initial. Din cate am prezentat pana acum, un QuadTree este infinit, dar pe noi ne intereseaza de obicei intervale foarte mici din plan, si atunci putem sa folosim numai cateva nivele din QuadTree. Cateodata unele noduri din QuadTree nu contin insa nici o informatie si atunci nu avem nevoie sa le folosim pentru ca am folosi memorie in plus.

In problema 3 a zilei 2 a Balcaniadei de Informatica din 1997, se da un QuadTree care reprezinta o imagine colorata alb-negru, de dimensiune 2^N * 2^N. Daca patratul reprezentat de informatia dintr-un nod al arborelui era de aceeasi culoare, in nod se pastra informatia culorii si nodul nu avea nici un fiu, altfel nodul avea starea indecisa/nedeterminata si avea patru fii.

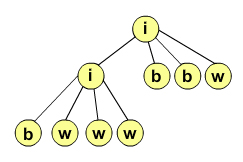
Prima imagine prezinta ordinea in care fii reprezinta patratele, a doua imagine reprezinta o imagine alb-negru, iar a treia este reprezentarea sub forma de QuadTree a acelei imagini.

Pentru a reprezenta n puncte de coordonate intregi in plan cu ajutorul structurii de QuadTree, vom insera care un punct pe rand in QuadTree. Pornim de la un QuadTree gol si inseram un nod recursiv, vedem pentru fiecare patrat care nu are latura de dimensiune unu in care din cele patru patrate din interiorul lui intra punctul nostru. Daca nu exista nod care sa reprezinte acel patrat, il creem noi.

Avantajul pentru structura de QuadTree este usurinta implementarii, dezavantajul este ca structura lui si timpul de raspuns la intrebari depind si de configuratia punctelor, nu numai de numarul total de puncte.

kD-Tree

kD-Tree este o structura de date care organizeaza o multime de puncte in k dimensiuni, imparte spatiul in semispatii astfel ca fiecare nod din arbore reprezinta un paralelipiped si contine in el un punct. Noi suntem interesati de arbori 2D in special. Pentru cazul 2D, primului nod ii va fi asociat intreg planul. Se duce o linie verticala de abscisa x care imparte planul in doua si punctele in doua multimi de cardinal egal. Subarborele din stanga va contine toate punctele din stanga acestei drepte verticale, iar subarborele din dreapta va contine toate punctele din dreapta acestei drepte verticale. Radacinei arborelui din stanga ii va fi asociat semiplanul stang determinat de dreapta verticala, si va contine punctul median dintre punctele din semiplanul stang sortate dupa y. Astfel, la nivel impar punctele vor fi mediane din sirul punctelor sortat dupa x, iar la nivel par punctele vor fi mediane din sirul punctelor sortat dupa y. Pentru mai multe dimensiuni ale spatiului ciclam dupa d₁, d₂,..., d_n si apoi iar d₁ ca sa punem elementul median pe nivelul curent. In cazul 2D complexitatea crearii unui asemenea arbore e O(n log n). Pentru a raspunde la query-uri pe un dreptunghi coboram in arbore in fii pentru care domeniul asociat se intersecteaza cu dreptunghiul nostru. Se poate demonstra ca aceasta operatie are timpul de executie in cel mai rau caz O(sqrt(n)).

Unele implementari tin puncte numai in frunze, si in nodurile care nu sunt frunze tin numai informatia despre coordonata dreptei care imparte regiunea in doua. Dimensiunile regiunii asociate unui nod pot fi tinute in nod sau pot fi calculate la fiecare operatie pentru a salva spatiu. O alta idee pentru a mari viteza de cautare in arbori kD ar fi sa nu alegem ciclic pe ce directie impartim punctele, ci sa alegem la fiecare pas directia pe care punctele sunt cele mai imprastiate.

Pseudocod pentru constructie: