Blog infoarena
Retrospectiva anului 2016
Anul 2016 mai are câteva ore până la final, aşa că avem o bună ocazie să ne amintim care au fost cele mai importante evenimente pentru comunitatea informatică din România, petrecute în decursul ultimelor 365 de zile. Ca de obicei, lista este pur subiectivă, aşa că vă invit să o com(ple|en)taţi pe forum.
Girl power
Să fi rezolvat România cea mai importantă problemă din informatică? Nu, nu mă refer la P vs NP, ci la faptul că ştiinţa calculatoarelor părea a nu fi un domeniu atractiv pentru fete. Ei bine, anul acesta, foarte multe dintre rezultatele bune la competiţiile naţionale şi internaţionale se datorează lor. Aşa că ar fi nedrept să nu le menţionăm aici, pe prima poziţie în lista noastră, şi să le felicităm cum se cuvine pe:
Alexa Tudose •Alexa2001 : Aur la JBOI, Argint la RMI, Bronz la Shumen (juniori), Locul I la ONI, Locul I la finala Algoritmiada juniori
Udristoiu Alexandra Maria •alexandra_udristoiu : Aur la JBOI, Argint la RMI, Argint la Shumen (juniori), Locul IV la ONI, Menţiune la finala Algoritmiada juniori
Cella Florescu •cella.florescu : Argint la JBOI, Locul I la ONI
Laura Georgescu •laurageorgescu : Bronz la RMI, Locul II la ONI, Menţiune la finala Algoritmiada seniori
Livia Magureanu •livlivi : Bronz la Shumen (seniori)
Maria Pandele •Smaranda : Locul I la ONI
Ana Kapros •akapros : Locul III la ONI
Deşi la IOI, CEOI şi BOI am trimis în continuare echipe compuse doar din băieţi, am o presimţire că în următorii ani acest lucru se va schimba şi că vom avea inclusiv o fată în echipa de IOI. O singură întrebare rămâne: cine va fi aceasta?
CEOI
La 7 ani după ediţia din 2009, CEOI a revenit în România, având loc în perioada 18-23 iulie la Piatra Neamţ. După ce Marian Darius •dariusdarius ne-a împărtăşit gândurile lui despre competiţie din punctul de vedere al concurentului, iată şi un inside view din partea mea, ca membru al comisiei:
- E greu să estimezi dificultatea unui set: credeam că vom avea punctaje de 100 pe problema Kangaroo din prima zi, şi măcar un scor mai mare de 29 pe problema Trick. Noroc că ne-am descurcat mai bine cu ziua 2. :)
- E mult mai multă presiune când eşti membru în comisie decât atunci când participi. Concurenţi, o să vă fie dor de vremurile bune.
- Melodia Trandafir de la Moldova era notificarea că un concurent a pus o întrebare.
- Am jucat prea mult Pokemon Go pentru binele nostru. Aveam inclusiv o problemă de rezervă cu tematică Pokemon.
- Să primeşti aprecieri de la liderul delegaţiei Poloniei produce un sentiment unic.
- Comisia a avut parte de o excursie la un baraj. Nu s-a făcut absolut nicio glumă pe acest subiect. ;)
Echipele României au obţinut şi ele rezultate frumoase la CEOI, dar despre asta în secţiunea următoare.
Rezultate internaţionale
La nivel de liceu, singurul lucru care ne-a despărţit de a avea un an excelent din punct de vedere al rezultatelor internaţionale a fost neobţinerea unei medalii de aur la IOI, lucru care nu s-a mai întâmplat din 2011. Poate că un lot aflat între generaţii, excesiv de "dopat" cu tehnici şi cu prea puţină experienţă la ad-hoc-uri explică această prestaţie mai modestă la cea mai mare competiţie internaţională. Cu toate acestea, rezultatele individuale ale membrilor loturilor sunt importante şi merită notate:
Oncescu Costin •geniucos : Argint la IOI, Aur absolut la BOI, Aur absolut la Shumen (seniori), Aur absolut la Yakutia şi Aur la RMI
Andrei Constantinescu •Andrei1998 : Argint la IOI, Aur la BOI, Aur la Shumen (seniori) şi Argint la RMI
Popa Andrei •andreiiii : Argint la IOI, Argint la BOI, Argint la Shumen (seniori) şi Aur la RMI
Radu Muntean •heracle : Bronz la IOI, Bronz la CEOI
Emanuel Nrx •StarGold2 : Argint la JBOI, Aur la Shumen (juniori), Argint la RMI
Marian Darius •dariusdarius : Aur la CEOI, Argint la Shumen (seniori)
Tatomir Alex •atatomir : Bronz la CEOI, Aur la RMI
Alexandru Petrescu •alexpetrescu : Argint la Shumen (seniori), Argint la Yakutia, Argint la RMI
Constantin-Buliga Stefan •fanache99 : Argint la CEOI, Bronz la Shumen (seniori), Bronz la RMI
Andrei Coman •andreicoman : Argint la Shumen (juniori), Bronz la RMI
Chiriac Andrei •chiriacandrei25 : Bronz la CEOI, Argint la RMI
Vlad Rochian •vladrochian : Argint la CEOI, Bronz la RMI
Iordache Ioan-Bogdan •iordache.bogdan : Bronz la Shumen (seniori), Argint la RMI
Tamio Vesa Nakajima •tamionv : Argint la BOI
sebi nechita •sebinechita : Bronz la CEOI
Harsan Razvan •hrazvan : Bronz la RMI
La nivel universitar, România este reprezentată pentru prima oară de către două echipe la finala ACM. Acestea sunt:
- Echipa Universităţii Politehnica din Bucureşti:
- Echipa Universităţii Bucureşti:
Nu în ultimul rând, trebuie să spunem că anul acesta trei români au ocupat locul I la concursuri online: Adrian Budau •freak93 a câştigat SRM 678 Div 1, iar
Oncescu Costin •geniucos şi
Constantin-Buliga Stefan •fanache99 au câştigat Codeforces Round #371 Div 1, respectiv Div 2.
Îi felicităm pe toţi şi le urăm mult succes pe anul ce urmează!
2017
Ce ne aşteaptă în 2017? Generaţia care a absolvit anul acesta nu a dat foarte mulţi membri în lot, aşa că preconizez că lotul lărgit va rămâne în mare parte constant, sperând şi la o creştere valorică a membrilor lui. Poate, de ce nu, să obţinem din nou o medalie de aur la IOI?
Vorbind despre IOI, competiţia va avea loc anul acesta la Teheran, aşa că poate ar fi util celor care au pretenţii de calificare să rezolve probleme propuse de iranieni (numeroase concursuri de pe Codeforces au fost propuse de aceştia).
În speranţa că cele câteva New Year's Resolutions de anul trecut (care, apropo, sunt valabile şi pentru anul acesta) v-au fost utile pe 2016, vă las şi acum câteva pentru anul ce urmează:
- Învăţatul de tehnici de programare este bun, până la un punct. Mai bine investiţi-vă timpul gândindu-vă la probleme de idee, ad-hoc-uri, decât în a învăţa cel mai rapid algoritm de FFT.
- Ca şi anul trecut, nu pot spune suficient de apăsat că participarea la concursuri este utilă: Algoritmiada, Codeforces, USACO, COCI, TopCoder, Mindcoding şi CSAcademy sunt doar câteva dintre cele la care puteţi să vă pregătiţi.
- Lucraţi mai organizat şi mai eficient: alegeţi-vă cu grijă problemele pe care le lucraţi, ca timpul pe care îl investiţi în pregătire să nu se irosească pe probleme uşoare.
În loc de încheiere, o previziune... numerologică: numere norocoase pe 2017: 3 şi 4.
La mulţi ani 2017!
Starea natiunii 2016 - Bun venit la scoala
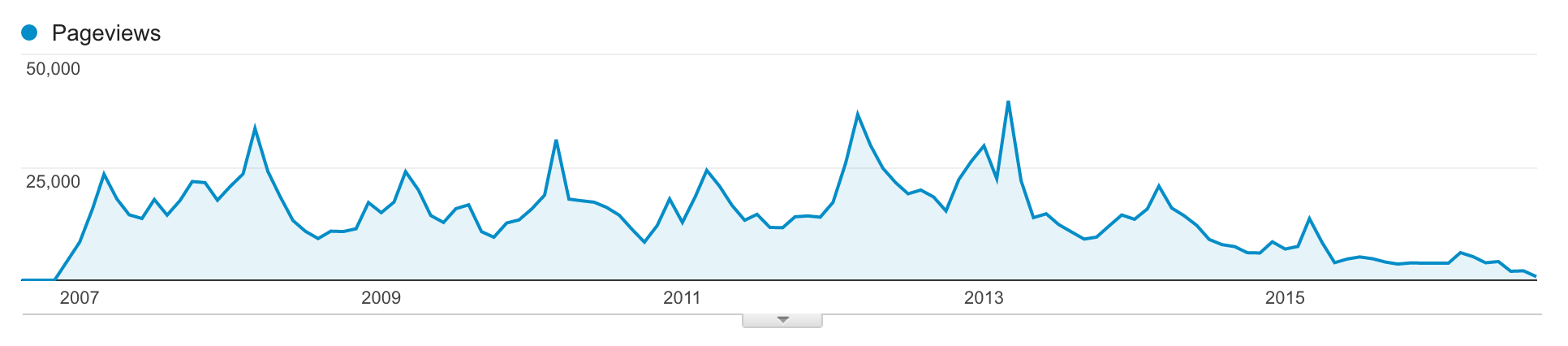
Infoarena creste ca trafic de la an la an. In total avem 70 de milioane de pageviews de cand strangem date pe google analytics (candva in 2007).
M-am gandit ca ar fi interesant sa ne uitam la niste date. Graficele au scara de inaltime diferita, deci nu se pot compara unul cu altul usor.

Forumul si-a pierdut din activitate. In jurul lui s-a format comunitatea infoarena. Pagina noastra de facebook https://www.facebook.com/infoarena/ are cateva postari (95% dintre ele puse de mine :) ) are aproape 3000 de likeuri, dar nu are o comunitate vibranta.
In schimb va recomand calduros clubul de info https://www.facebook.com/groups/349814335155898/ All the cool kids are there.
Pe blog primeam initial 100 si ceva de views pe articol. 200 daca articolul era mai popular. O data ce am inceput sa avem grup pe facebook adaugam linkul si pe pagina pe facebook. Primim de acolo 700 - 1000 de vizite.
Pozele cu echipa romana la IOI primesc in jur de 3000 - 5000 de vizite. E continutul preferat de cei ce au dat like la pagina infoarena. Linkuri cu articole despre olimpici in ziare de circulatie mare din nou sunt foarte apreciate pe pagina noastra de facebook.
De-a lungul timpului discutam in interiorul echipei despre modalitati de a creste comunitatea. O idee era sa facem siteul in engleza pentru ca deja am atins toti elevii pasionati de info din tara.
In 2011, 2012 am incercat sa scriu mai frecvent, sa am invitati pe blog. Apoi am vrut sa testez ideea cu comunitatea internationala si am inceput sa scriu in engleza. Rezultatele au fost foarte interesante, am adus cititori noi. Dar ei nu ramaneau si nu deveneau mebrii ai comunitatii. Puteti observa experimentul in graficul traficului pe blog:

Cele mai populare articole pe blog:
- blog/numbers-everyone-should-know
- blog/oji-kit-3
- blog/meet-in-the-middle
- blog/square-root-trick
- blog/sfaturi-pentru-interviuri
- blog/rolling-hash
- blog/girls-programming-camp-2011
- blog/interviu-mihai-patrascu-partea-intai
- blog/cum-sa-scrii-un-cv
Blog posturile in engleza le-am postat pe reddit. Cate unul imi lua in jur de 10 ore de munca. Am avut in 2 zile in jur de 100 000 de pageviews petru Numbers Everyone Should Know.
 Pe blog avem in total 780 000 de views. Raspunsurile mele pe quora au rezultate mai bune.
Pe blog avem in total 780 000 de views. Raspunsurile mele pe quora au rezultate mai bune.
Sunt bucuros ca csacademy a luat ideea cu comunitatea internationala in serios.
Alta optiune pentru infoarena ar fi sa fie mai putin elitista. Asa a aparut arhiva educationala, care e una dintre cele mai populare parti ale siteului. Pe aceasi directie pbinfo facut de profesorul Silviu Candale de la Colegiul National "Liviu Rebreanu", Bistrita e o resursa foarte buna pentru elevii ce lucreaza informatica la clasa.
Grafic bonus - articole

Cam atat :). Sper ca v-au placut statisticile.
Bun venit la scoala, la cat mai multe probleme rezolvate!
Finala Algoritmiada 2016
Finala Algoritmiada 2016 va avea loc în perioada 22-24 septembrie, la Cluj. În acelaşi timp şi spaţiu are loc şi Finala ONIS. Finala Algoritmiada va avea loc Vineri, 23 septembrie, iar Finala ONIS va avea loc Sâmbătă, 24 septembrie. Un program complet al weekend-ului respectiv va apărea în curând :).
Puteţi găsi aici lista cu concurenţii calificaţi la runda finală. Criteriile de calificare fiind uşor mai complicate decât în trecut, iar informaţiile de pe conturile concurenţilor fiind deseori incomplete, este posibil ca lista să conţină greşeli. Rugăm toţi concurenţii interesaţi de desfăşurarea finalei să verifice lista şi să ne semnaleze eventualele greşeli. Puteţi vedea criteriile de calificare în runda finală aici. Lista va fi considerată finală Duminica, 11 septembrie, la ora 23:59.
Calificati Juniori:
Calificati Seniori:
Ganduri despre Central European Olympiad in Informatics
Dupa cum mi-am format un obicei, desi de data asta cu putina intarziere, voi face un topic legat de concursul CEOI 2016. In primul rand, rezultatele Romaniei au fost:
Romania 1:
Radu Muntean - 179, locul 20, bronz
Alex Tatomir - 180, locul 19, bronz
Vlad Rochian - 292, locul 8, argint
Bogdan Iordache - 134, locul 31
Romania 2:
Darius Marian - 359, locul 5, aur
Sebastian Nechita - 187, locul 17, bronz
Stefan Buliga - 268, locul 10, argint
Andrei Chiriac - 155, locul 25, bronz
Felicitari tuturor!
Dupa cum am facut si pentru BOI 2015, respectiv Yakutia 2015 si 2014, voi scrie si cateva impresii / experiente personale legate de acest concurs:
- Eu am intalnit pentru prima oara o problema de tipul "Multi-run", in care programul scris se evauleaza de mai multe ori, cu fiecare run pe alt input, iar unele run-uri pe input egal cu outputul generat de o rulare anterioara. Acest stil s-a manifestat aici prin problema "Trick" din prima zi, in care trebuia sa joci pe rand rolul a doi asistenti si apoi a unui magician ce se folosea de ce ii spuneau cei doi asistenti. Nu trebuie sa te gandesti foarte mult pentru a iti da seama ca acest sistem deschide usa spre o gama foarte larga de probleme superbe, printre care dupa parerea mea si aceasta. Problema insa a fost ca "Trick" era putin prea grea, sau poate mai bine zis, nu chiar potrivita unui concurs pe sistemul 3 probleme in 5 ore. Se poate vedea din rezultate, unde cativa insi au reusit formidabilul scor de 29 de puncte, restul fiind toti cu 0.
- Tot in ziua 1 au mai fost o problema de dinamica "Cangur" si o problema interactiva "Icc" care nu se poate incadra foarte bine in vreo tehnica. Cangur era din nou o problema destul de frumoasa, cu o reducere de la O(N3) la O(N2) intr-un loc foarte neasteptat, insa din nou, dupa parerea mea, foarte grea (nimeni nu a reusit la concursul on-site sa rezolve problema integral, scorul maxim fiind de 51 de puncte pe ea pentru O(N^3)). Problema "Icc" aducea insa putin balans setului, fiind o problema "relativ" usoara, cand comparata cu celelalte 2. Aceasta au facut-o majoritatea medaliatilor. Apare totusi o problema cand exista o singura problema accesibila intr-un concurs: foarte multe scoruri egale. Dupa prima zi, locurile 4-9 aveau cu totii 151 de puncte. Overall, o zi frumoasa, dar se putea si mai bine.
- In ziua 2 insa, lucrurile s-au schimbat destul de radical. Problema "usoara" nu a facut-o locul 1. Problema "grea" a facut-o locul 25 (bine Chiriac Smile ). Problema medie au facut-o 4 sau 5 insi. Ce mi s-a parut interesant era ca toate 3 erau cel putin accesibile, adica concurentul "mediu" al concursului putea face in 5 ore cel putin una dintre probleme, indiferent care. Mi se pare ca problemele au fost mult mai bine alese in ziua 2 fata de ziua 1, atat pentru departajare (nicio egalitate de punctaj in primele 17 de locuri) cat si pentru experienta placuta a concurentului.
- Totusi, nici ziua 2 nu a fost perfecta. Problema "Match" avea limita scrisa gresit in enunt (N <= 106 in loc de 105), iar cu limita de 0.15 secunde era greu de crezut ca s-ar vrea O(N * sigma) nu O(N). Drept urmare, la concursul online, un polonez a rezolvat problema in O(N), mai bine decat solutia comisiei, luand in acelasi timp 300 in ziua respectiva (wow). De asemenea, testele nu erau cele mai bune, pentru ca desi toate solutiile implementate in concurs se comportau foarte bine in practica, fiecare avea un anumit "Edge-case" care mergea in O(N^2) (de a mea nu sunt sigur, inca nu am gasit ceva ce sa mearga prost, dar sigur exista). Full feedback pe 4 probleme din 6, super tare.
Una peste alta, concursul a iesit bine. Nu incape nici o indoiala. Pentru mine cel putin, a fost cel mai bun concurs international la care am participat vreodata. Nu doar ca rezultat, cat si ca experienta de concurs, experienta in afara concursului, socializare, tot. Multe felicitari comisiei (tuturor comisiilor), probleme superbe, putine `scapari`, si alea relativ mici, organizare buna, oras frumos, tot ce trebuia. O seara faina!
Lights out - shortlist
In 2005 I used to write some articles for Ginfo (the romanian informatics gazzette, targeted towards highschool and university cs students). Each article contained a set of problems that were all related in their solution or setup. Quite a few of those articles are on infoarena as well, you can find them by looking for titles that start with "Probleme cu" in the article section (only in romanian).
Writing one of those articles used to take me quite some time, and I have a few drafts remaining. Instead I've resorted to writing shortlists. I write the problems and people solve some of them in the comments :).
I was talking to my friend Slava Gurevich today and he reminded me of this set of problems that I was meaning to write about 10 years ago. So thanks Slava :).
The problems are based on the game Lights Out. They were used in various romanian and other international contests. They vary in difficulty from technical interview level to university coding contest.
Give them a try in the comment section:
- (technical interview) You are given a 3×3 grid of light bulbs. Some lights are “on”, and some are “off”. Next to each light there is a button. Pressing that button results in toggling the state of both the current light and its four adjacent lights (left, right, up down). For a given configuration find the minimum number of button presses such that all the lights are “off”.
- (training LOT98) You are given a grid of lights of size NxM (N, M <= 1000). Some lights are “on”, some are “off”. A move consists in choosing a rectangle of size PxQ and toggling the state of all the lights in that rectangle. Come up with an algorithm that finds the minimum number of moves that turn all the lights off.
- (OJI9*) Again, you are given a grid of NxM lights, that can be either “on” or “off”. One move consists in choosing a row or a column in this grid and toggling the states of all the lights in that row or column. Come up with an algorithm that finds the minimum number of moves to switch all the lights “off”.
- (LOT9*) Same problem as 1, but the grid size is 20×100.
- (LOT95) You are given a tree of n <= 1000000 nodes and n - 1 edges. Each node of the tree contains a light bulb and a button. Pressing the button in a node switches the state of the light bulb and the adjacent light bulbs. Come up with an algorithm that finds out the minimum number of button presses to switch all the light bulbs “off”
- (SGU) You are given an undirected graph of n <= 100 nodes. Each node contains a light bulb and a button. Pressing the button in a node toggles the state of the light bulb and its adjacent light bulbs. Come up with an algorithm that finds out if there is any solution that turns all the lights “off”.
- (SGU/TOPCODER) Same setup as 6. Come up with an algorithm that finds out how many different solutions there are.
- (LOT06) You are given a grid of lights of size NxM (N, M <= 1000). Some lights are “on”, some are “off”. A move consists in choosing a cell and switching the state of the lights on the same row and same column but leaving the chosen cell in the same state. Come up with an algorithm that finds out the minimum number of moves to turn all the lights “off”.
- (CEOI 2000) Planet-X
Why didn't neural networks work back in 1986
Neural nets have been around for quite some time. They have become popular only in the last few years. How come?
Geoffrey Hinton quickly addresses the question in his talk

Watch the entire talk!
All aboard the deep learning train and Alien Labs
I've been thinking about deep learning ever since I saw Andrew Ng's talk at Google back in 2012, but somehow never made much progress other than talking to people.
Deep learning has recently ~2010-2012 become very effective across a large set of problems where progress was very slow. It would be a shame not spending some time on it.
I think the infoarena community should move some of it's focus from solving algorithm puzzles to machine learning and deep learning in particular.
Here are some of my notes about this:
Anecdotes:
- Doing object recognition used to be a hard problem. If you need a car detector, you would hire five PhDs and let them work on it for a few years. Now it's a solved problem, even your phone has a strong enough computer to do a good job.
- Google voice was unusable for me a few years ago, now it gets my bad English accent.
- DeepMind f*king solved Go. A game which 2 years ago was thought to be 10 years out of reach.
- Object detection is real time, one can use it for self driving cars, the radar solution might be getting outdated.
- Baidu is working on speech recognition for mandarin (lots of illiterate people with phones).
- Word embeddings give you natural language models that do away with the tweaks one used to encode all sorts of idiosyncrasies in the English language.
Shallow field OpenAI CTO: "As Ilya likes to say, deep learning is a shallow field — it's actually relatively easy to pick up and start making contributions.
- deep learning techniques started to be effective recently (2010? 2012?)
- you can do a lot without being a hard core mathematician
- the field is still a bit of an art so coding contest guys shouldn't feel bad about tweaks and hacks
- previous experience in the old techniques is not very relevant
- a home setup or some AWS resources are enough to start (a google datacenter of GPUs would help)
- state of the art results significantly improving on the previous state of the art
(in real time object detection, speech recognition)
Interesting concepts:
- Word2Vec - neat idea that maps words to points in n dimensional space. Then you can do algebra on the vector representation:
vec(“king”) – vec(“man”) + vec(“woman”) =~ vec(“queen”), or vec(“Montreal Canadiens”) – vec(“Montreal”) + vec(“Toronto”) resembles the vector for “Toronto Maple Leafs” (Mikolov, Tomas; Sutskever, Ilya; Chen, Kai; Corrado, Greg S.; Dean, Jeff (2013). Distributed representations of words and phrases and their compositionality)
- Back propagation - I see it as a dynamic programming technique that works well for the neural network setup to compute partial derivatives one needs when running gradient descent
- Convolutional neural networks - a convolutional layer reuses the same k weights instead of having k^2 weights between 2 layers (this concept makes sense in image input and makes algorithms much faster)
- Rectified Linear Units f(x) = max(0, x) work much better than the historically used sigmoid and hyperbolic tangent functions
- Dropout - some neurons are ignored with a set probability, inspired by how the neurons in the brain aren't always on
Some deep learning news:
- 2016 ACRush, 3 times Google Code Jam winner, joins Baidu to work on autonomous cars
So coding contest guys are getting in the field :). - Introducing OpenAi
"these funders have committed $1 billion, although we expect to only spend a tiny fraction of this in the next few years." - 2014 Baidu started a deep learning lab, Andrew Ng and other Stanford people went there
- 2014 Oxford natural language processing research group bought by Google
- 2014 Google acquired DeepMind for more than 500 million dollars. That's how much it costs to beat Go
- 2013 Facebook starts a deep learning lab
- 2013 Wired interview with Geoff Hinton, one of the neural net pioneers
- 2012 Google cat detector on 16000 machines
And some news:
Mircea Pasoi and Cristian Strat, after their successful stint at Twitter, recently founded Alien Labs. They use deep learning to build intelligent chat bots for an office environment. This is an awesome opportunity to work together again. It's been 8 years since we last did. At Google, we worked on an ads inventory management problem using network flows Our claim to fame is that we got help from Cliff Stein, the S in CLRS :). This is also an opportunity for me to jump on the deep learning train while tackling real world problems.
Yesterday I've started at Alien Labs based in San Francisco. The first thing I'm going to work on is figuring out if two questions are similar. This should be fun!
Here's the Alien Labs website , have a look.
I'll follow up with a few posts on deep learning that may encourage you to try it if you haven't already.
Problem: Shoe laces
Here's a probability puzzle I've learned from Alex Ku:
There are N shoe laces in a bag. A move consists of randomly picking two shoe lace ends from the bag, tying them together and then placing them back in the bag. We keep going until we can't find any shoe lace ends to tie. What is the expected number of different shoe lace cycles we'll have at the end.
P.S. Please don't spoil the problem if you've seen it before.
ONIS 2016 Runda 1 Editorial
Prima rundă de calificare a concursului ONIS 2016 s-a încheiat. În cele ce urmează vom prezenta o scurtă analiză a concursului, însoţită de soluţiile oficiale ale problemelor propuse.
În primul rând, felicitări câştigătorilor! Mai exact, primelor cinci echipe de studenţi în ordinea clasamentului:
1. UPB Banu Popa Visan •team_name
3. UNIBUC Kira96 lockmihai •corul_barbatesc
4. UBB Cociorva Popoveniuc Salajan •lookingForAChallenge
5. UNIBUC Impaler-009 Challenge costyv87 •The_Viper_The_Mountain_And_The_Imp
De-asemenea, primelor 5 echipe de liceu:
2. Tamio Vesa Nakajima •tamionv
4. UVS Babalau Rochian Tarniceru •enterprise
5. UNIBUCThrowTerror •Spiromanii_Messi
Încă o rundă de felicitări pentru UPB Banu Popa Visan •team_name, singurii care au reuşit să rezolve toate cele 9 probleme din set şi pentru
Oncescu Costin •geniucos, care a reuşit să iasă de unul singur pe locul 2, după ce o bună perioadă din concurs a condus clasamentul.
Concursul a început după cum era de aşteptat cu submisii la problema A. MaxSubSum. Conform tradiţiei, surprinzător de mulţi concurenţi au trimis soluţii care nu foloseau tipuri de date pe 64 de biţi. Atragem atenţia aici şi asupra faptului că tipul long nu are 64 de biţi pe platforma noastră. După cum puteţi citi (spre exemplu) aici, este o soluţie mult mai bună să folosiţi mereu tipul long long, care nu variază la fel de mult în funcţie de arhitectură. Participanţii la OJI să ia aminte :)
A urmat problema F. Pokemon, ca dovadă că enunţurile lungi/complicate nu implică neaparat soluţii lungi/complicate, o lecţie valoroasă pentru majoritatea concursurilor de informatică. Pentru idei de optimizare, puteţi citi aici despre cum operaţiile pe mulţimi se împacă foarte bine cu operaţiile pe biţi.
Problema C. Minlcm avea nevoie de observaţia că e mai productiv să iterăm peste posibilii divizori comun, decât peste un membru al perechii şi de ideea folosirii unui ciur pentru a o implementa eficient. Mai avea nevoie şi de întregi pe 64 de biţi :).
Problema D. Unlock necesita în primul rând puţină imaginaţie pentru a crea un test în care soluţia brută chiar se comportă foarte prost (idei?). Apoi, era nevoie de o soluţie care se amortiza peste mărimile tuturor componentelor colorate şi o implementare grijulie. Nimeni nu a reuşit să rezolve aceasta problemă din prima submisie, deci ar fi cazul să ne şlefuim puţin abilităţile de implementare :).
Apropo de implementare, un skill care pare să lipsească aproape universal participanţilor este acela de a-şi simplifica ideile înainte de a le implementa sau de a căuta de la început idei care să permită o implementare concisă. În cazul de faţă, problemele G. Puzzle2, B. Avioane2, E. Min Max Store şi într-o anumită măsură D. Unlock se pretau la a fi "supra-implementate".
Problema I. Nucleul Valoros 2 avea nevoie de o optimizare subtilă a recurenţei descrise în enunţ. Puteţi găsi aici un blogpost în care sunt enumerate mai multe metode utile de a optimiza anumite tipuri de recurenţe.
În continuare, aveţi soluţiile problemelor în detaliu :).
A. MaxSubSum
Algoritmul general de determinare a submatricei de sumă maximă este prea încet pentru această problemă, având complexitate O(N ^ 3). Este în schimb natural să ne gândim că putem obţine o soluţie mai rapidă dacă analizăm modul de construcţie al matricei. Astfel, analizând matricea cu colţurile (x1, y1, x2, y2), observăm că suma sa este (x2 - x1 + 1) * B[y1...y2] + (y2 - y1 + 1) * A[x1...x2], unde prin T[a...b] am notat suma T[a] + T[a + 1] + …. T[b]. Această formulă ne arată, printre altele, că nu este întotdeauna optim să alegem independent liniile şi coloanele matricei bazându-ne pe subsecvenţele de sumă maximă din cele două şiruri (soluţie încercată iniţial de unii concurenţi). Uneori o subsecvenţă de sumă nemaximă, dar de lungime mare, poate fi de ajutor.
În schimb, este adevărat că dacă submatricea optimă va avea X linii şi Y coloane, ne intereseaza doar subsecvenţele de lungime X, respectiv Y care au suma maximă posibilă în A şi B. Putem precalcula uşor şirul bestA[Length] = “suma maximă a unei subsecvenţe din A de lungime Length ” în timp O(N2), analog pentru şirul bestB[]. Apoi vom itera peste toate cele N2 dimensiuni posibile ale submatricei şi vom reţine maximul expresiei LineCount * bestB[ColumnCount] + ColumnCount * bestA[LineCount].
Numarul de echipe care au rezolvat problema: 73
Prima echipa care a rezolvat problema: Oncescu Costin •geniucos
B. Avioane2
Construim 3 tipuri de evenimente:
- Decolare: Decoleaza avionul cu indicele X din aeroportul A la timpul Td
- Aterizare: Aterizeaza avionul cu indicele X din aeroportul B la timpul Ta
- Query: Raspundem la un query pentru aeroportul C, timpul Tq
Sortam evenimentele in functie de timp si simulam un algoritm de drum minim, pas cu pas in functie de ce evenimente apar. La orice moment de timp, tinem pentru fiecare nod X costul minim de a junge din nodul 1 in nodul X.
- Eveniment query (aeroportul C): raspunsul este costul minim curent de a ajunge din 1 in C, pur si simplu trebuie afisat.
- Eveniment de Decolare (aeroportul A): costul minim de a ajunge intr-o anumita destinatie poate sa fie modificat cu costul minim de a ajunge in momentul de fata in nodul din care decolam (nodul A) + pretul biletului pentru acest avion. In cazul in care aceasta varianta se va dovedi a fi mai buna, vom actualiza costul minim pentru destinatie in momentul aterizarii
- Eveniment de Aterizare (aeroportul B): selectam pentru nodul in care aterizam (nodul B) cea mai buna varianta (ori pastram costul minim de pana acum, ori costul obtinut prin intermediul avionului care tocmai a aterizat, cost calculat la evenimentul de tip Decolare)
Problema poate fi vizualizata ca si un caz particular al algoritmului de Bellman-Ford. Din moment ce avem si axa timpului, este suficient sa trecem o singura data prin muchii deoarece o muchie cu un cost mic la un anumit moment de timp nu poate afecta alte configuratii la timpi mai mici
Numarul de echipe care au rezolvat problema: 29
Prima echipa care a rezolvat problema: Oncescu Costin •geniucos
C. MinLcm
Folosim proprietatea: cmmmc(a, b) = a * b / cmmdc(a, b)
Din moment ce a, b <= 100.000, avem garantia si ca cmmdc(a, b) <= 100.000
Se observa faptul ca pentru un cmmdc fixat D, ne intereseaza cele mai mici 2 elemente din sir care au acest D drept divizor (pentru a minimiza a * b / D). Aceste 2 numere se pot calcula simplu pentru fiecare divizor D cu ajutorul ciurului lui Eratostene.
Obsevatie: Algoritmul fixeaza in realitate doar un divizor al celor 2 numere (fără a avea vreo garanţie că este cmmdc-ul real), dar dacă divizorul respectiv nu este într-adevăr cel mai mare posibil al celor două numere, va produce un rezultat mai mare decât cel real, deci răspunsul problemei nu va fi afectat.
Numarul de echipe care au rezolvat problema: 32
Prima echipa care a rezolvat problema: UNIBUC Suditu Cornoiu Chihai •forsakenAwe
D. Unlock
O primă soluţie posibilă este cea de a itera pe rând prin toate cele K culori şi a efectua câte o parcurgere a matricei pentru a verifica dacă celulele libere sunt conexe. Această soluţie are complexitate worst-case O(N * M * K), iar date fiind limitările lui K, este echivalentă cu O((N * M) 2). Deşi la prima vedere ar părea că este puţin probabil ca atât K cât şi zonele atinse de fiecare parcurgere să fie de mărime Θ(N * M) simultan, există teste în care acest lucru se întâmplă, iar soluţia descrisă depăşeşte cu mult limita de timp, care, mai mult, este calibrată pentru a procesa 25 de teste, nu unul singur.
Pentru a obţine o soluţie mai rapidă, vom încerca ca pentru fiecare culoare fixată să depunem efort (i.e număr de operaţii) proporţional cu numărul total de celule de această culoare. Deoarece în total acest număr este limitat de N * M, complexitatea ar fi şi ea proporţională cu această valoare. Pentru a construi o asemenea soluţie, vom face pentru început nişte parcurgeri care vor identifica zonele conexe de celulele libere. Apoi, pentru fiecare culoare fixată, fie ea C, vom face o parcurgere pentru fiecare componentă conexă de culoare C şi vom reţine cu ce zone conexe libere este vecină fiecare astfel de componentă. Dacă o anumită componentă Comp de culoare C este vecină cu zonele libere “x1, x2 .. xT”, atunci aceste zone vor deveni conectate în momentul în care o facem pe Comp accesibilă. Astfel, pentru fiecare componentă îi putem uni vecinii cu o structură de date eficientă (de tip păduri de mulţimi disjuncte), iar la final trebuie ca toate zonele libere iniţiale să fie conexe. Pentru a justifica faptul că numărul de operaţii este proporţional cu mărimea componentelor de culoare C, observăm faptul că fiecare zonă liberă vecină cu o anumită componentă trebuie să fie adiacentă cu componenta respectivă pe cel puţin o latură a unei celule din componentă. Deoarece numărul de laturi al unei componente conexe este limitat de 4 * (mărimea componentei), rezultă că numărul maxim de vecini distincţi posibili este limitat de aceeaşi valoare.
Este nevoie de o implementare atentă pentru a menţine complexitatea dorită. Spre exemplu, reiniţializarea completă a pădurilor de mulţimi disjuncte pentru fiecare culoare poate duce din nou la timp O((N * M)2), chiar dacă restul algoritmului este eficient.
Numarul de echipe care au rezolvat problema: 15
Prima echipa care a rezolvat problema: Gangster Teddy Bears Trio •UNIBUC_Costan_Iordache_Magureanu
E. MinMaxStore
Se observa faptul ca proprietatea este independenta pentru minim si maxim.
Initial consideram ca toate cele N valori sunt posibile minime. In momentul in care avem o operatie Store(A, B), aplicam urmatorii pasi:
- Daca A este posibil minim, ramane posibil minim
- Daca A nu este posibil minim, acesta devine posibil minim doar daca B este posibil minim.
- B nu mai poate sa fie minim orice ar fi
La sfarsit proprietatea este adevarata daca avem un singur posibil minim si acesta se afla pe pozitia indicata. Analog facem si pentru maxim si raspundem la fiecare din cele 4 cazuri in functie de corectitudinea celor 2 raspunsuri.
Numarul de echipe care au rezolvat problema: 30
Prima echipa care a rezolvat problema: UNIBUC Harsan Bicsi Baltatu •echipa_BoSSilor
F. Pokemon3
În ciuda enunţului mai complex, aceasta este una dintre cele mai simple probleme la nivel algoritmic. Deoarece numărul de tipuri de pokemon este mic, putem itera prin toate submulţimile posibile de pokemoni şi verifica pentru fiecare submulţime dacă aceasta asigură victoria. Pentru a se încadra în timp, soluţia trebuie să codeze submulţimile ca măşti de biţi şi să facă verificarile folosind operaţii pe biţi pe aceste valori. Complexitatea finală este O(2 N * N).
Numarul de echipe care au rezolvat problema: 69
Prima echipa care a rezolvat problema: UPB Banu Popa Visan •team_name
G. Puzzle2
Problema admite multe soluţii, care variază mai ales ca dificultate a implementării. O soluţie rezonabilă vine din observaţia că o dată ce am aflat prima linie a matricei, restul matricei se poate reconstitui cu uşurinţă, linie cu linie. Pentru a construi prima linie, putem începe dintr-un colţ (un nod cu 2 vecini) şi parcurge numai noduri de margine (care au 3 vecini) până găsim un alt colţ. Dacă alegem să facem acest lucru, trebuie să tratăm special cazul matricelor cu 2 linii (sau coloane), deoarece în acest caz parcurgerea nodurilor de margine poate alterna haotic între cele două linii, fără ca lanţul obţinut în final să fie o linie reală a matricei. Cazul se tratează uşor, observând că acum un colţ este vecin direct cu cel puţin un alt colţ. Cele două colţuri vor forma singure prima linie, iar acum putem reconstitui restul matricei ca în cazul general. Un alt caz particular, dar foarte simplu, este cazul unei matrice cu o singură linie.
Numarul de echipe care au rezolvat problema: 21
Prima echipa care a rezolvat problema: Oncescu Costin •geniucos
H. Subpermutari
Consideram toate cele N2 subsecventele are permutarii noastre. Observam faptul ca daca pentru o secventa [a,b] determinam cea mai lunga subpermutare care este atat prefix, cat si sufix a secventei noastre, putem foarte usor marca sufixul ca fiind o secventa care a mai aparut deja si crestem frecventa prefixului.
Pentru a determina cea mai lunga subpermutare care este atat prefix, cat si sufix, vom aplica un algoritm foarte asemanator KMP-ului:
Fixam pozitia de start a subsecventei noastre si pornim algoritmul de KMP de acolo.
Presupunem ca avem calculat pentru o subsecventa [a,b] acest cel mai bun prefix-sufix (il notam identic ca la KMP cu pi[b]). Cand vrem sa trecem la urmatorul element, b + 1, avem aceleasi 2 cazuri de luat in considerare ca si la KMP:
Cazul in care elementul inserat b + 1 are aceelasi indice in subpermutarea sufixului ca si urmatorul element in subpermutarea prefixul: pur si simplu pi-ul creste cu 1
Daca indicele difera, micsoram pi-ul (mergem in pi[pi[b]]) si repetam procedeul pana avem o potrivire
Pentru a determina al catelea element se afla o valoare intr-o secventa putem usor precalcula cu un simplu aib.
Complexitate: O(N2 log N)
Numarul de echipe care au rezolvat problema: 2
Prima echipa care a rezolvat problema: Oncescu Costin •geniucos
I. Nucleul Valoros Season 2
Pornim de la solutia brute, programare dinamica in O(N3).
D[i][j] = costul minim al secventei [i,j]. Recurenta este data in enunt: fixam un k de la i la j - 1 si luam cea mai buna varianta
Notam pentru un interval [i,j], valoarea k pentru acest interval drept optim[i][j].
Prima proprietate foarte importanta este faptul ca: optim[i][j - 1] <= optim[i][j] <= optim[i + 1][j]
Intuitiv este foarte usor de vizualizat acest lucru:
Daca am secventa [i, j - 1] si adaug un element nou in dreapta, k se poate muta doar la dreapta
Daca am secventa [i + 1, j] si adaug un element nou in stanga, k se poate muta doar la stanga
O sa demonstram ca daca facem for dupa k de la optim[i][j - 1] pana la optim[i + 1][j], in loc sa il facem de la i la j, obtinem complexitate O(N2).
Demonstratie: Consideram toate intervalele de lungime x. Avem proprietatea optim[a][b - 1] <= optim[a][b] <= optim[a + 1][b] si optim[a + 1][b] <= optim[a + 1][b + 1] <= optim[a + 2][b + 1], unde b - a + 1 = x. Observam ca sfasitul unui interval de lungime x este inceputul urmatorului interval de lungime x. Amortizat, obtinem O(N) pentru fiecare lungime x de interval, O(N2) in total.
Numarul de echipe care au rezolvat problema: 13
Prima echipa care a rezolvat problema: UPB Banu Popa Visan •team_name
AGM 2016
Am placerea de a anunta faptul ca povestea merge mai departe ! Dupa o prima editie in care initiativa unui grup restrans de oameni (si in special de elevi) din Colegiul National "Spiru Haret" din capitala a fost sustinuta de Youth Bank, Concursul National de Informatica "Adolescent Grigore Moisil" revine cu o a doua editie, de data aceasta cu mentiunea ca acum este inclus acum în Calendarul Concursurilor Naţionale Şcolare ale MECS. Cea de-a doua editie va avea loc pe 26 martie..
De mentionat este faptul ca acum, la sustinerea concursului, contribuie patru mari companii din Romania : Emag (prin Fundatia Emag), Siveco Romania , Qualitance si Rodl & Partner. Evident, invariantul in toata aceasta poveste este comunitatea Infoarena care continua sa sprijine organizarea concursului si sa incurajeze initiativele similare!
Acest concurs se desfasoara pe format ACM-ICPC, noutatea fiind data de faptul ca se adreseaza elevilor de liceu. Echipele pot fi de maxim 3 elevi (toti membrii unei echipe fiind, obligatoriu, legitimati la acelasi liceu).
Neconventional este si modul in care concurentii vor fi cazati: acestia vor beneficia de cazare in familile voluntarilor din Colegiul National "Spiru Haret", acest lucru insemnand conditii mult mai bune decat ceea ce am fi putut obtine la un camin din Bucuresti cat si garantia sigurantei concurentilor pe toata durata desfasurarii concursului.
Legat de numarul de echipe participante, pot spune ca acesta este unul mai mult decat generos, in concurs fiind primite 25 de echipe. Din cauza faptului ca laboratoarele liceului nu permit un numar mai mare de echipe participante, concursul va fi si online, gazduit de Infoarena.
Link-ul pentru inscriere este : http://goo.gl/forms/WIXIU3SsyP
Termenul limita pentru inscriere este 15 martie.
Site-ul competitiei este : http://agminformatica.wix.com/agminfo
Tin sa le multumesc sponsorilor (Siveco Romania si Fundatia Emag), lui Adrian Budau •freak93,
Mihai Calancea •klamathix si
Eugenie Daniel Posdarascu •eudanip (care ne-au sarit in ajutor cand a venit vorba de organizarea concursului si care ne-au sprijinit initiativa), dar si celor 6 membrii ai comisiei stiintifice din care fac si eu parte :
Florin Elfus •florin.elfus,
Lucian Bicsi •retrograd,
Stavarache Petru Eric •ericpts,
Chichirim George •george_stelian,
Ionescu Teodor •teoionescu si
George Marcus •PlayLikeNeverB4. De asemenea, un merit important in organizarea concursului il are directiunea Colegiului National "Spiru Haret" care s-a implicat foarte mult in dezvoltarea acestui proiect.
Numai bine si keep coding!

