Rezolvare pentru "suma in triunghi" si functii convexe

Cosmin Negruseri
21 decembrie 2011

Functiile convexe sunt functiile pentru care graficul lor se afla sub orice segment de dreapta ce uneste doua puncte ale graficului. Mai formal, avem ca daca f:X->R unde x e un domeniu convex (interval etc.) atunci pentru oricare doua puncte x1 si x2 din X si orice t din intervalul [0, 1] avem ca f(tx1 + (1-t)x2) <= tf(x1) + (1-t)f(x2).

E simplu de demonstrat ca suma a doua functii convexe e tot o functie convexa. Functiile strict convexe au proprietatile interesante ca ele au doar un minim local care este si global si ca maximul pentru o functie convexa e realizat pe marginea domeniului de definitie.

Rezolvare
In cazul problemei noastre, functia distanta e o functie strict convexa si o combinatia din problema 2dist(M, A) + dist(M, B) + dist(M, C) este si ea o functie convexa. Si cum maximul pentru functii de genul asta e realizat in capete, ne e deajuns sa ne uitam la valoarea functiei in punctele A, B si C. Astfel vedem ca C e punctul cautat.

Am vrut sa vad cum se comporta functia si am facut un grafic folosind octave.

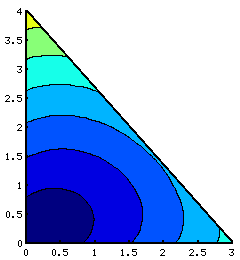
Daca A, B si C au coordonatele (0, 0), (3, 0), (0, 4) se observa usor ca punctul C minimizeaza functia noastra.

In machine learning apare frecvent problema de minimizare a valorii unei functii. Cele mai multe functii nu sunt usor de minimizat. Nu au o forma care poate fi rezolvata matematic sau sunt neregulate si au multe optime locale. Pentru a putea obtine solutii bune, de multe ori functiile astea sunt aproximate sau marginite de functii convexe pentru care exista algoritmi buni de minimizare, cel mai simplu ar fi gradient descent.
Functiile convexe sunt folositoare in multi algoritmi folositi in machine learning. De multe ori e nevoie sa se obtina un punct ce minimizeaza cate o functie. D

dist = @(x, y, x1, y1) sqrt((x - x1).^2 + (y - y1).^2)
sumt = @(x, y) 2 * dist(x, y, 0, 0) + dist(x, y, 3, 0) + dist(x, y, 0, 4)
x=linspace(0, 3, 50)
y=linspace(0, 4, 50)
[xx,yy]=meshgrid(x,y)
contourf(xx,yy,sumt(xx,yy))