Coding contest byte: Meet in the middle

Cosmin Negruseri
10 august 2012

Meet in the middle (sometimes called split and merge) is a clever approach which tries to trade off space for time. Much like divide et impera it divides the problem in two and then tries to merge the results. The benefit is that by using quite a bit of memory you can tackle problems of twice the size you could before.

Here are a few applications.

4sum

Given A, an array of integers, find out if there are any four numbers in the array that sum up to zero (the same element can be used multiple times). For example given A = [2, 3, 1, 0, -4, -1] a solution is 3 + 1 + 0 - 4 = 0 or 0 + 0 + 0 + 0 = 0.

The naive algorithm checks all four number combinations. This solution takes O(N⁴) time.

A slightly improved algorithm brute forces through all n³ three number combinations and efficiently checks if -(a + b + c) is in the original array using a hash table. This algorithm has O(n³) complexity.

By now, you’ve probably started thinking how the meet in the middle technique could be applied to this problem. The trick is to rewrite the equation as: a + b = -(c + d). Store all the n² sums a + b in a hash set S. Then iterate through all n² combinations for c and d and check if S contains -(c + d).

Here's how the code looks

def 4sum(A):
  S = {}
  for a in A:
    for b in A:
      S[a + b] = (a, b)

  for c in A:
    for d in A:
      if -(c + d) in sums:
        print (S[-(c + d)][0], S[-(c + d)][1], c, d)
        return

  print "No solution."

This algorithm has O(n²) time and space complexity.

Breaking 2DES

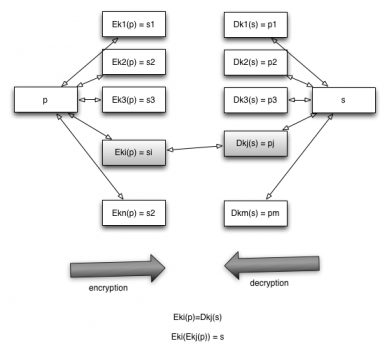DES is an encryption standard which uses 56 bit keys. Today computers can use a brute force approach to break the encryption. One simple approach to make the encryption more secure is to apply it twice, using two different keys. This approach is susceptible to the meet in the middle attack developed by Diffie Hellman. 3DES is less susceptible as it encrypts the message three times using 3 keys.

Let’s see why 2DES is vulnerable. Let Ek be the encryption function using the secret key k and Dk the decryption function using the secret key k. 2DES uses Ek1) = s to encrypt and Dk2) = p to decrypt.

Diffie Hellman’s meet in the middle attack trades off space for time to find out the two secret keys.
For the pattern p it tries all the possible keys to obtain a set of numbers corresponding Ek(p). Also for the pattern s it uses all the possible keys to decrypt s, Dk(s).
If we find any match in the two sets it means that Ek1 = Dk2 so the secret keys are k1 and k2.
The naive brute force algorithm would go through 2⁵⁶ * 2⁵⁶ iterations by brute forcing through all possible values of k1 and k2 while this algorithm uses 2⁵⁶ * 56 memory to store Ek(p) and does 2⁵⁶ work to find a match.

Discrete logarithm

Given n a prime number and p, q two integers between 0 and n-1, find k such that p^k = q (mod n).

This problem can be solved using the baby step, giant step algorithm which uses the meet in the middle trick.
We can write k = i([sqrt(n)] + 1) + j
Notice that i <= sqrt(n) and j <= sqrt(n).
Replacing k in the equality we get p^{(i ([sqrt(n)] + 1) + j)} = q (mod n).
Dividing by p^j we get p^{(i[sqrt(n)] + 1)} = qp^-j (mod n).
Using meet in the middle becomes obvious. We can brute force through the numbers on each side of the equality and find a colision.
The algorithm takes O(sqrt(n)) space and O(sqrt(n)) time.

Bidirectional search

Find the shortest path between two nodes nodes in a large graph which you can’t keep in memory, for example the Facebook friendship graph.

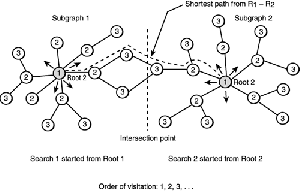The usual approach is to use a bread first search algorithm. If the distance between two nodes is k and the average degree in the network is p then we explore O(p^k) nodes.

One neat idea is instead of starting the search from one node, start from both and see when the two search spaces meet. This way we only go through O(p^k/2) nodes.

This approach works well on both path finding problems on explicit graphs and on implicit state graphs like ones in games.

Caveats

Unlike divide and conquer the trick in meet in the middle can't be applied recursively because the sub problems don't have the same structure as the original problem.
Bidirectional search can be often replaced by some search algorithm that uses some heuristics like A*.

Additional problems

1. Friend of a friend(interview question): Given two user names in a social network find design an efficient way to test if one is a friend of a friend of the other.
2. Equal partition: Given a set A of 40 real numbers, find out if there is any way to split A in two sets such that the sums of their elements are equal. (Hint: complexity O(2^n/2))
3. Minimal vertex cover: Given a graph of n nodes (n <= 30), find out a set with the smallest number of vertices such that each edge in the graph has at least one node inside the set. (Hint: complexity O(3^n/2))
4. Square: You're given an array L which represents the sizes of n planks. You have to answer if there's any way to form a square using the planks without breaking them of overlapping them. (Hint: complexity O(4^n/2))
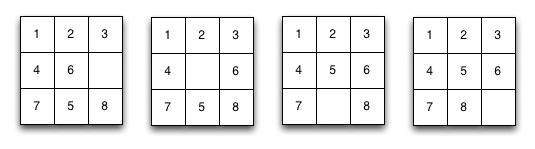
5. 8 puzzle: The 8 puzzle is a sliding tile puzzle of 3×3 slots with 8 tiles and one empty slot. At each step you can move one of the orthogonally neighbouring tiles to the empty slot. The game starts from a random initial configuration and the purpose is to get to the * in the fewest number of moves. Figure out an efficient algorithm that solves the 8 puzzle. (Hint: Each position is solvable in at most 31 moves) In the picture we see a sequence of moves that solves the puzzle.
   

Try the to solve these problems in the comment section.