Cautarea ta binara e gresita

Cosmin Negruseri
07 ianuarie 2012

Cautarea binara e probabil primul algoritm studiat de elevii sau studentii la informatica care exemplifica tehnica divide and conquer. Ea rezolva problema gasirii unui element x in un sir sortat A. Ideea de baza e simpla: folosindu-ne de monotonia datelor putem reduce la fiecare pas problema la jumatate. Totusi aproape fiecare concurent olimpiada de informatica are cate o poveste cum a bushit o problema din cauza unei cautari binare. La fel in interviurile de programare marea majoritatea a canditatilor nu reusesc sa scrie o cautare binara care sa mearga corect pe toate cazurile.

Apar buguri frecvente cum ar fi intrare in ciclu infinit, algoritm gresit pentru siruri de scurte de lungime 0, 1, 2, pentru siruri in care x nu exista sau x apare de mai multe ori.

Ideea de baza e ca vom folosi un invariant in bucla cautarii binare. Pentru cazul nostru acesti invariant e ca lo indica spre un element care e mai mic ca x sau spre -1 si hi indica spre un element mai mare sau egal cu x sau in A.length. Pe scurt $A[lo] < x \le A[hi]$ (consideram $A[-1] = -\infty$ si $A[A.length] = +\infty$ )

Sa vedem cum arata codul:

int search(int[] A, int x) {
    int hi = A.length, lo = -1, mid;
    while (hi - lo > 1) {
        mid = (lo + hi) / 2;
        if (A[mid] < x)
            low = mid;
        else
            hi = mid;
    }
    if (hi == A.length || A[hi] != x)
        return -1;
    else
        return hi;
}

Invariantul este $A[lo] < x \le A[hi]$ (pentru simplitate consideram $A[-1] = -\infty$ si $A[A.length] = +\infty$ ). La fiecare pas injumatatim distanta intre lo si hi. Observam ca invariantul face ca lo sa fie tot timpul diferit de hi si astfel conditia continuare e hi - lo > 1 nu hi - lo > 0. Cand hi si lo sunt consecutive putem lua o decizie, sa returnam A[hi] daca x e in sir sau -1 daca x nu apare in sir.

O data ce ati inteles ideea de mai sus, veti vedea cum puteti schimba invariantul usor pentru a rezolva probleme ca gasirea ultimei aparitii a lui x in sirul sortat, gasirea predecesorului lui x in sir sau gasirea succesorului.

Aceasta abordare e detaliata in cartea Prgramming Pearls de Jon Bentley.

Apar tot felul de variante, de exemplu unii testeaza daca a[mid] e egal cu x si scurt circuiteaza cautarea. Aceasta optimizare nu ajuta in cazul general, doar complica codul. Alta varianta e ca poti reduce ceva mai mult problema folosind hi = mid - 1 sau lo = mid + 1. Pentru mie e putin mai greu de verificat invariantul cautarii, avand un pas logic in plus. Pe langa asta cazurile in care ajungem la una din marginile sirului pot deveni mai dificile.

O solutie folosita frecvent de membrii infoarena foloseste puterile lui 2. Puteti vedea ca arata destul de misto:

int binary_search(int A, int val) {
  int i, step, N = A.length;
  for (step = 1; step < N; step <<= 1);
  for (i = 0; step; step >>= 1)
    if (i + step < N && A[i + step] <= val)
    i += step;
  return i;
}

Mie nu imi place aceasta varianta. Un dezavantaj e ca un programator are nu stie trucul intelege codul de mai sus mai greu.

Daca v-am suparat cu linkbaitul din titlu :), va mai zic ca in 2006, Joshua Bloch, cel care a scris algoritmul de cautare binara in java.util.Arrays a descoperit un bug in implementare bug care aparea in majoritatea cautarilor binare sau a sortarilor prin interclasare scrise in ultimii 20 de ani. Pe scurt, lucrand la Google el a ajuns sa sorteze siruri de doua miliarde de numere. Astfel pasul mid = (lo + hi) / 2 a ajuns sa depaseasca Integer.MAX_VALUE care e 2147483647. Putem rezolva bugul folosind 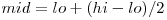$mid = lo + (hi - lo) / 2$ in loc de $mid = (hi + lo) / 2$ .

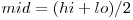In urmatorul articol voi discuta ce probleme pot aparea la cautarea binara pe numere reale sau metoda bisectiei cum mai e numita.

Voi ati avut vreodata probleme cu cautarile binare? Ce varianta folositi?

Categorii:

infoarena informatica de performanta

Ultimele insemnari

Categorii

Blogroll

Cautarea ta binara e gresita