Revizia anterioară Revizia următoare
Automate finite si KMP
(Categoria Algoritmi, Autor Adrian Vladu)
In acest articol vom aborda cele mai comune probleme legate de pattern matching si vom oferi suportul teoretic necesar intelegerii algoritmului Knuth-Morris-Pratt, pornind de la potrivirea standard cu automate finite si rafinand-o treptat pana la un algoritm de complexitate O(n + m). Toate acestea intr-o maniera usor de inteles ;)
Automate finite
Ce sunt automatele finite ?
Un automat finit este definit ca un cvintuplu <Q, q0, A, Σ, δ> unde Q este o multime finita de stari Q = {q0, q1, ... qn}, q0 apartine Q (q0 = stare initiala), A inclus in Q (A = multimea starilor de acceptare), Σ este un alfabet, iar functia δ : Q x Σ -> Q este functia de tranzitie a automatului.
Aceasta este definitia matematica si foarte abstractizata a automatelor. Pentru a le intelege mai usor, sa luam un exemplu concret
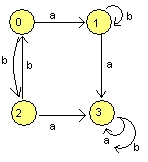
- Q = {q0, q1, q2, q3}
- A = {q3}
- Σ = {a, b}
- δ =
| δ | a | b |
| 0 | 1 | 2 |
| 1 | 3 | 1 |
| 2 | 3 | 0 |
| 3 | 3 | 3 |
Ce inseamna asta? Sa spunem ca automatul primeste un string s = bbaba
Initial ne aflam in q0. Pentru fiecare element al stringului si facem tranzitia δ(qk, si).
Pornim din k = 0. Vom avea :
- k = 0; δ(0, b) = 2;
- k = 2; δ(2, b) = 0;
- k = 0; δ(0, a) = 1;
- k = 1; δ(1, b) = 1;
- k = 2; δ(1, a) = 3;
Daca ultima stare obtinuta qk apartine A, atunci spunem ca automatul accepta stringul. Altfel spus, daca avem stringul s, lungime(s) = n, automatul accepta stringul daca si numai daca δ( ... δ( δ(0, s1), s2 ) ..., sn ) apartine A.
Stringurile 'aa', 'aaaaaaa', 'aabababab', 'aaaba', 'ba', 'aba' sunt acceptate de automat, dar 'abbbbbb', 'bba' nu.
La ce folosesc ?
- Inteligenta artificiala (prima si cea mai involuata stare a inteligentei artificiale)
- Aplicatii teoretice si probleme de matematica :)
- Pattern matching
Se dau stringurile M si N. Se cere sa gasim toate aparitiile lui N in M.
Vom numi Mi prefixul lui M de lungime i. Presupunand ca avem construit automatul care accepta stringul N, vom cauta toate prefixele lui M acceptate de automat, deci toate numerele 1 ≤ i ≤ lungime(M) cu proprietatea ca automatul accepta stringul Mi.
Algoritm_potrivire_cu_automat_finit
n = lungime(N)
q = 0;
pt i <- 1, n
q = d(q, M[i])
daca q apartine A
scrie "potrivire la pozitia " i - n + 1- Complexitate : O(n)
Sa vedem cum se construieste automatul de potrivire pentru un string N. Fie m = lungime(M). Construim un automat cu m + 1 stari {q0, q1, ... qm}, A = {qm} . Faptul ca ne aflam in starea x inseamna ca au fost acceptate primele x caractere din sirul de intrare.
Din fiecare stare qx apartine Q si pt fiecare c apartine S construim δ(x, c) = y cu proprietatea ca My este cel mai lung prefix al lui M care este sufix al lui Mxc (prefixul de lungime x al lui M, concatenat cu caracterul c).
Algoritm_constructie_automat_finit
m <- lungime(M)
pt q <- 0, m
pt c apartine S
gaseste M[i] = cel mai lung prefix al lui M cu M[i] sufix al lui M[q]c
d(q, c) = i- Complexitate : linia 4 are complexitatea O(m2) (implementata in maniera bruta) si se executa de (m + 1) * |Σ| ori => complexitate totala O(m3 * |Σ|)
Practic, algoritmul calculeaza pentru toate 0 ≤ i ≤ m, c apartine S cat de mult putem lua de la sfarsitul lui Mic astfel incat acesta sa fie un "inceput" de N.
Acesta se poate rafina, eliminand operatii redundante, dupa cum vom vedea in cele ce urmeaza.
Algoritmul KMP
Gaseste toate aparitiile unui string N in M in timp O(n + m), unde n = lungime(N), m = lungime(M). O parte esentiala a sa este functia prefix π : {1..n} -> {0..n-1} unde πi = cel mai lung prefix al lui M care este sufix al lui Mi. Evident, Mπi (prefixul de lungime πi al lui M) este prefix al lui Mi, deci πi < i.
Algoritm_calcul_functie_prefix
n <- lungime(N)
k <- 0
pi[1] <- 0
pt i <- 2, n
cat timp (k > 0) si (N[k + 1] != N[i])
k <- pi[k]
daca N[k + 1] = N[i]
k <- k + 1
pi[i] <- kAnaliza complexitatii :
- la fiecare pas (i = 2, n) k se incrementeaza cel mult o data, deci pe parcursul algoritmului k se va incrementa de cel mult n - 1 ori (linia 8)
- in linia 5, k se decrementeaza cel mult pana devine 0, deci se va decrementa de cel
mult n - 1 ori pe parcursul algoritmului - ⇒ Complexitate : O(n)
Algoritmul este similar cu constructia automatului de acceptare. Din fiecare stare i in care s-a acceptat Ni, vedem cat de mult putem lua de la sfarsitul lui Ni astfel incat sufixul respectiv sa fie prefix pentru N. De remarcat ca in cazul in care starea candidata k nu este buna, nu mergem in k - 1, ci in πk. Aceasta este de fapt "magia" care ofera complexitate liniara.
Algoritmul de potrivire este similar celui al calculului functiei prefix, numai ca aici la fiecare pas i cautam cel mai lung prefix al lui N care este sufix al lui Mi.
Algoritm_potrivire_KMP
m <- lungime(M), n <- lungime(N)
q <- 0
pt i <- 1, m
cat timp (q > 0) si (N[q + 1] != M[i])
q <- pi[q]
daca N[q + 1] = M[i]
q <- q + 1
daca q = n
scrie "potrivire la pozitia " i - n + 1Analog Algoritm_Calcul_Functie_Prefix, complexitatea algoritmului efectiv de potrivire este O(m). Astfel rezulta complexitatea liniara a algoritmului KMP O(n + m)
Teme pentru acasa:
- folosind functia prefix, rafinati constructia automatului finit de acceptare pentru un string, aducand-o la complexitatea O(m2 * |Σ|)
- problema Microvirus (hint : construiti automatul de potrivire pentru stringul dat)
- Timus 1158: Censored!
