Revizia anterioară Revizia următoare
Solutia problemei Tablou
Concurentul Theodor Moroianu •theodor.moroianu s-a oferit sa descrie solutia sa la aceasta problema:
Subtask 1:
Salvam intr-o matrice tridimensionala tablourile fiecarei fete:
Mat[id][i][j] este culoarea de pe pozitia (i, j) din tabloul fetei id.
In 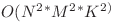 calculam diferenta ceruta.
calculam diferenta ceruta.
Subtaskurile 2,3:
Majoritatea solutiilor din subtaskurile acestea sunt:
- Optimizari ale solutiei din Subtaskul 1
- Solutii bazate pe frecventa cifrelor 0...9
- Solutii ne-optimizate din Subtaskul 4 bazate pe observatia prezentata tot acolo
Subtask 4:
Exista diferite solutii care sa ia 100 de puncte, complexitatea cea mai putin eficienta care sa intre in timp fiind
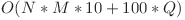
O sa analizam mai departe o solutie cu complexitatea 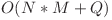
Observatia de baza pentru aceasta solutie este ca suma ![\sum_{B,a,b,p,q}^{} A[a][b]-B[p][q] \sum_{B,a,b,p,q}^{} A[a][b]-B[p][q]](http://www.infoarena.ro/static/images/latex/9ff0d5b404d2a2881cee28483d47b98d_5.36115pt.gif) poate fi scrisa sub forma
poate fi scrisa sub forma ![N*M*(\sum_{a,b}^{} A[a][b]-\sum_{p,q}^{} B[p][q]) N*M*(\sum_{a,b}^{} A[a][b]-\sum_{p,q}^{} B[p][q])](http://www.infoarena.ro/static/images/latex/599d0b12e6a9fa3d79acc7a5b778680d_5.36115pt.gif)
Raspunsul pentru o anumita poza poate deci fi scris sub forma ![\sum_{poza B!=a}^{} {N*M*(\sum_{a,b}^{} A[a][b]-\sum_{p,q}^{} B[p][q])} \sum_{poza B!=a}^{} {N*M*(\sum_{a,b}^{} A[a][b]-\sum_{p,q}^{} B[p][q])}](http://www.infoarena.ro/static/images/latex/ad70dab5ee793dcaf68417a8da11ba6a_5.36115pt.gif)
![= N*M*Q* \sum_{a,b}^{}{A[a][b]}-N*M*\sum_{poza B!=a}^{} {(\sum_{p,q}^{} B[p][q])} = N*M*Q* \sum_{a,b}^{}{A[a][b]}-N*M*\sum_{poza B!=a}^{} {(\sum_{p,q}^{} B[p][q])}](http://www.infoarena.ro/static/images/latex/d7efda2391f8179a2e22e29d93942f63_5.36115pt.gif)
Astfel, pozitiile / frecventele valorilor din imagini nu ne mai intereseaza, vrem doar sa stim suma lor!
Fie 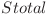 suma tuturor elementelor tuturor pozelor, si
suma tuturor elementelor tuturor pozelor, si ![s[i] s[i]](http://www.infoarena.ro/static/images/latex/90ce10bc65abeaa3715038c6647c5fbd_3.5pt.gif) suma elementelor din poza i.
suma elementelor din poza i.
Raspunsul pentru o poza  o sa fie
o sa fie ![N*M*(Q*s[i] - (Stotal-s[i])) N*M*(Q*s[i] - (Stotal-s[i]))](http://www.infoarena.ro/static/images/latex/1c86438fd0d48e63194d4273a73ab3ca_3.5pt.gif) .
.
Solutie alternativa
Aceasta este solutia autorului.
Vom nota cu S = 10 numarul de cifre in baza 10, altfel spus marimea alfabetului cu care sunt descrise tablourile, pentru conturarea complexitatilor solutiilor ce urmeaza:
Pentru 10 puncte
Solutia de complexitate  timp si
timp si  memorie nu face decat sa creeze cele Q tablouri si sa calculeze conform enuntului costul fiecaruia. Se fixeaza tabloul caruia vrem sa ii calculam costul, de unde un factor de
memorie nu face decat sa creeze cele Q tablouri si sa calculeze conform enuntului costul fiecaruia. Se fixeaza tabloul caruia vrem sa ii calculam costul, de unde un factor de  , se fixeaza tabloul cu care il comparam, alt
, se fixeaza tabloul cu care il comparam, alt  , se fixeaza pozitia (a, b) in
, se fixeaza pozitia (a, b) in 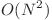 si pozitia (p, q) in
si pozitia (p, q) in 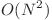 , si se adauga la raspuns diferenta intre cele 2 caractere.
, si se adauga la raspuns diferenta intre cele 2 caractere.
Pentru 30 - 50 de puncte
Prima observatie ce poate fi facuta e ca putem scurta mult calculul dereglarii a doua tablouri daca, in loc sa consideram toate pozitiile cu toate poitiile, le grupam in functie de cifra lor. Cu alte cuvinte, e suficient sa cunoastem sirul fr[t][0...9] care ne spune, pentru tabloul t, cate cifre de 0, de 1, ..., de 9 are in el.
Astfel, putem calcula, parcurgand fiecare tablou, acest sir fr[t][0...9]. Cand vrem sa calculam dereglarea dintre tablouri, e suficient sa fixam cifra c1 din primul tablou t1 si cifra c2 din al doilea tablou t2 si sa adunam la valoarea primului tablou fr[t1][c1] * fr[t2][c2] * (c1 - c2). Complexitatea este  timp si
timp si  memorie.
memorie.
Pentru 60 de puncte
O alta observatie ce poate fi facuta este ca nu trebuie sa obtinem explicit fiecare tablou pentru a calcula sirul sau fr[0...9]. Este suficient sa stim sirul asociat tabloului initial al lui Marcel si cate cifre de 0, de 1, ..., respectiv de 9 se afla in submatricea unde se recoloreaza cu culoarea cul. Pentru a cunoaste aceasta, e suficient sa precalculam un tablou de sume partiale pentru fiecare cifra in parte, astfel:
S[ c ][i][j] = numarul de cifre c din submatricea cu coltul stanga-sus in celula (1, 1) si coltul dreapta-jos in celula (i, j).
S[ c ][i][j] = S[ c ][i - 1][j] + S[ c ][i][j - 1] - S[ c ][i - 1][j - 1] + (1 daca T[i][j] = c, 0 daca nu)
Calculul acestui tablou tridimensional are complexitate 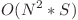 atat ca timp, cat si ca memorie.
atat ca timp, cat si ca memorie.
Atunci cand vrem sa calculam sirul fr[0...9] al unui anumit tablou, putem copia frecventa cifrelor din cel initial, apoi putem scadea din fr[ c ] numarul de cifre egale cu c din submatricea recolorata, adica S[ c ][lin2][col2] - S[ c ][lin2][col1 - 1] - S[ c ][lin1 - 1][col2] + S[ c ][lin1 - 1][col1 - 1]. La final, adaugam (lin2 - lin1 + 1) * (col2 - col1 + 1) la fr[cul].
Complexitatea solutiei este  timp si
timp si  memorie, intrucat pentru calculul valorii fiecarui tablou vom proceda asemanator cu solutia precedenta.
memorie, intrucat pentru calculul valorii fiecarui tablou vom proceda asemanator cu solutia precedenta.
Pentru 100 de puncte
Observatia finala se bazeaza pe faptul ca dereglarea dintre doua tablouri t1 si t2 este egala cu deregalarea dintre t1 si tabloul lui Marcel minus dereglarea dintre t2 si tabloul lui Marcel. (Vectorial, am putea spune ca 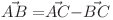 ).
).
Astfel, putem calcula in  dereglarea dintre fiecare tablou si tabloul lui Marcel, pe care o notam cu V[t]. Fie sum suma tuturor acestor dereglari V[t]. Atunci valoarea unui tablou este egala cu V[t] * K - sum.
dereglarea dintre fiecare tablou si tabloul lui Marcel, pe care o notam cu V[t]. Fie sum suma tuturor acestor dereglari V[t]. Atunci valoarea unui tablou este egala cu V[t] * K - sum.
Complexitate finala:  timp si
timp si  memorie.
memorie.
