Revizia anterioară Revizia următoare
Solutia problemei Panza
Solutia pleaca de la construirea unui tablou bidimensional d, in care d[i][j] are semnificatia urmatoare: lungimea minima a unui drum care pleaca din punctul S de pe primul segment, ajunge pe segmentul i in punctul j si trece prin fiecare interval cu vitamine pentru toate segmentele de la 1 la i. Astfel putem simula constructia unui drum de lungime cat mai mica. Pentru initializare, d1[i] = |i - S|, pentru calcul efectiv, vom folosi recurenta ce urmeaza sa fie descrisa, iar pentru raspunsul final vom fi interesati in valoarea minima ce poate fi obtinuta alegand convenabil o valoare pos si gasind solutia d[N][pos] + |pos - F|.
Pentru recurenta, presupunand ca am calculat d[i - 1][p], pentru oricare p intre X[i - 1] si Y[i - 1], vom dori sa calculam d[i][j], pentru oricare j intre X[i] si Y[i]. Trebuie sa fim atenti, deci, sa nu consideram drumuri care nu iau vitamina i sau i - 1.
Relevant pentru recurenta este pozitia p a carei valoare d[i - 1][p] o consider, cat si pozitia q unde folosesc puntea de lungime A[q]. In functie de acestea, putem scrie ca:
d[i][j] = minim {d[i - 1][p] + |p - q| + A[q] + |q - j|}, considerand orice q de la 1 la M si orice p de la X[i - 1] la Y[i - 1].
In functie de cat de eficient este realizata aceasta decizie de minim, se pot obtine solutii de mai multe complexitati ca timp:
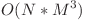- 30 de puncte
Se fixeaza p si q si se alege, dupa recurenta descrisa, solutia cea mai buna.
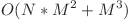- 70 de puncte
Se observa ca daca il fixam pe p, aflarea celui mai bun q, adica minimizarea lui |p - q| + A[q] + |q - j|, nu tine cont de i, deci putem precalcula tabloul r[j][p] cu semnificatia: care e cea mai mica valoare |p - q| + A[q] + |q - j|, alegandu-l convenabil pe q.
Astfel, precalcularea are complexitatea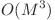 
pentru ca pentru ca fiecare j si p incercam toate pozitiile q.
De asemenea, recurenta devine:
d[i][j] = minim {d[i - 1][p] + r[j][p]}
Prin urmare, la fiecare i si j, iteram doar prin Y[i - 1] - X[i - 1] + 1 optiuni de valori ale lui p, adaugand la complexitate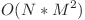 
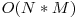- 100 de puncte
Ne bazam pe faptul ca Ai-1 ≤ Ai, pentru orice i. De asemenea, vom face cateva calcule intermediare de complexitate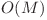 
pentru fiecare segment, astfel:
Mai intai calculam x[j] care e costul minim sa ajung in punctul j pe segmentul i - 1, stiind ca prin punctul j trec, pe punctea de lungime A[j], pe segmentul i. Pentru inceput, x[j] = d[i - 1][j], daca X[i - 1] ≤ j ≤ Y[i - 1], sau infinit daca nu. Apoi facem o parcurgere de la 2 la M si zicem x[j] = min {x[j], x[j - 1] + 1}. Apoi facem o parcurgere de la M - 1 la 1 si recalculam x[j] = min {x[j], x[j + 1] + 1}. Astfel, simulam o plimbare pe segmentul i - 1.
Apoi calculam y[j] = x[j] + Aj, adica am trecut prin puntea j pe segmentul i. Apoi facem o parcurgere de la 2 la M si zicem y[j] = min {y[j], y[j - 1] + 1}. Apoi facem o parcurgere de la M - 1 la 1 si recalculam y[j] = min {y[j], y[j + 1] + 1}. Astfel, simulam o plimbare pe segmentul i.
Acum, nu ne mai ramane de facut decat sa notam ca d[i][j] = y[j] daca X[i] ≤ j ≤ Y[i], sau infinit daca nu.
De observat ca aceste calcule pot fi facute cu un singur sir d[1...M], nefiind nevoie nici de tabloul bidimensional d, nici de x sau y.
