Solutii Algoritmiada 2010, Runda Finala

• Lista de probleme
• Lkperm
• Produs
• Matricen
• Inversari
• Conexiuni
• Covor
• Stalpisori
• ExpectedPos
• Risc
• Diagonala

Lkperm

Fie 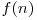numărul total de permutări de n elemente care respectă proprietatea din enunţ. În momentul în care dorim să calculăm 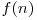, vom încerca să plasăm elementul maxim, adică pe n. Dacă el este plasat pe prima poziţie a permutării, atunci ea va arăta aşa:
n x₁ x₂ x₃ ... x_n-1
Elementul n va fi maximul doar pentru secvenţa n x₁ x₂ ... x_L-1. Aşadar, în acest caz sunt 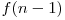posibilităţi.

Dacă plasăm elementul n pe cea de-a doua poziţie, permutarea va arăta aşa:
x₁ n x₂ x₃ ... x_n-1
Elementul n va fi maximul pentru două secvenţe, iar x₁ poate lua orice valoare între 1 şi n-1, deoarece el nu poate fi maximul în nicio secvenţa. Aşadar, există posibilităţi.

Dacă plasăm elementul n pe cea de-a p-a poziţie, 1 ≤ p ≤ K permutarea va arăta astfel:
x₁ x₂ x₃ ... x_p-1 n x_p+1 x_p+2 ... x_n-1
Elementul n va fi maximul pentru p secvenţe, iar primele p-1 elemente nu vor fi maxime în nicio secvenţă. Prin urmare vor fi 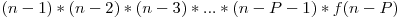posibilităţi

Aşadar, 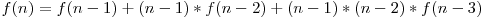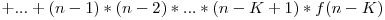, dacă
, altfel
Implementarea directă a acestei formule aduce 40 de puncte, deoarece are complexitatea O(N*K). Pentru 100 de puncte vom încerca să restrângem egalitatea şi observăm că

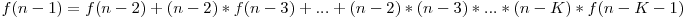
Deci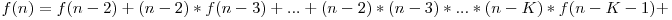

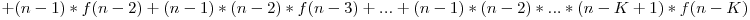
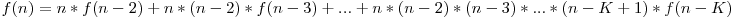
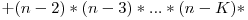
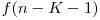
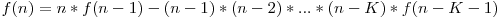
Produs

Deoarece întotdeauna exista soluţie numărul P = X * (X + 1) * (X + 2) * ... * Y. Deci ştim sigur ca numărul se poate descompune în factori primi mai mici decât 100000. Astfel putem descompune numărul şi apoi sa îl logaritmăm.

REZ = 0 ;
X = Y = 1 ;
cat timp ( REZ != log (P) )
    daca ( REZ < log (P) )
        REZ += log (X++)
    altfel
        REZ -= log (Y++)

Matricen

Inversari

Pentru a determina numărul de inversiuni dintr-un interval, vom menţine o matrice D[i][j] = numărul de inversiuni în intervalul de lungime i care are ca ultim element poziţia j. Relaţia de recurenţă este D[i][j] = D[i-1][j-1]+numărul de elemente din intervalul curent mai mari decât cel de pe poziţia j. Pentru a determina acest număr vom menţine o dinamică I[i][j] = numărul de elemente mari mari decat cel de pe pozitia j din intervalul de lungime i ce are pe ultima poziţie poziţia j. Recurenţa este I[i][j] = I[i-1][j], dacă elementul de pe poziţia j-i+1 este mai mic decât cel de pe poziţia j, sau I[i-1][j]+1 invers.

Se observă că, pentru cele două matrici nu avem nevoie decât de două linii, deci odată calculată matricea pentru o lungime de interval, vom răspunde la toate query-urile ce corespund acelei lungimi.
Complexitatea totală este O(N²+Q).

Conexiuni

Problema se rezolvă prin programare dinamică, mai precis D[i][j] este lungimea celei mai lungi secvenţe comune ce se termină pe poziţia i în primul şir, respectiv pe poziţia j în al doilea şir. Recurenţa este D[i][j] = D[i-1][j-1]+1, dacă A[i] = B[j], sau 0 altfel. Odată ce am determinat pentru poziţiile i şi j cea mai lungă secvenţă, este clar că va trebui să adunăm la rezultat toate secvenţele ce au lungimea între 1 şi cea mai mare lungime. Complexitatea finală este O(N*M). Problema mai admite si o alta solutie bazata pe algoritmul KMP, tot in complexitate O(N*M), care obtine 100 puncte. O alta solutie bazata pe Rabin-Karp, desi mentinand complexitatea la O(N*M), merge in practica foarte greu datorita operatiilor modulo care trebuiesc efectuate si se pare ca nu poate obtine prea usor 100 puncte.

Covor

Fie T[i][j] cea mai lungă secvenţă continuă cu 0 de pe linia i, având ca ultim element (i, j). Numărul de matrice pline cu 0 ce au în colţul dreapta-jos elementul (i, j) este T[i][j](cele de înalţime 1) + min(T[i][j], T[i-1][j])(cele de înălţime 2) + ... + min(T[i][j], T[i-1][j], ..., T[1][j])(cele de înalţime j). Implementarea directă a acestei relaţii are complexitatea O(N³) şi aduce 50 de puncte.
Pentru a obţine complexitatea O(N²), vom parcurge elementele pe coloane şi vom menţine o stivă ordonată crescător cu elementele din matricea T. Suplimentar, pentru fiecare element, vom reţine şi pentru câţi dintre termenii sumei prezentate anterior va fi elementul minim. Astfel, când dorim să introducem elementul T[i][j] în stivă, vom elimina elementele mai mari decât el şi vom adăuga la numărul asociat acestui element numerele asociate elementelor eliminate. La fiecare pas se adaugă la rezultat suma produsului dintre fiecare element din stivă şi numărul asociat lui.

Stalpisori

Pentru fiecare stalp i ne dorim sa gasim intevalul [st,dr] de lungime K astfel incat distanta D[i]=max(v[dr]-v[i],v[i]-v[st]) sa fie minima posibila. Avand calculate st si dr pentru stalpul i,cand vrem sa calculam pentru i+1 indicii st si dr pot doar avansa,asadar rezultand o complexitate O(N). Solutia D va fi maximul dintre toate D[i].

O alta solutie ce ar fi obtinut in jur de 70pct este de a cauta binar solutia.

ExpectedPos

Vom interclasa şirurile date şi vom obţine un şir mare ce conţine toate elementele ordonate crescător. În momentul în care vrem să vedem suma poziţiilor elementelor din fiecare query, vom căuta binar în şirul mare poziţia pe care s-ar afla elementul în acest şir, iar la poziţia găsită vom adăuga K-1, deoarece avem K şiruri, iar indexarea începe de la 1. Pentru a determina fracţia ireductibilă cerută, vom aplica Algoritmul lui Euclid.

Risc

În primul rând vom sorta nodurile după risc, şi le vom renumerota în ordinea crescătoare a riscului. Apoi sortăm şi query-urile după riscul maxim. Acum, vom parcurge nodurile în ordinea renumerotării şi vom aplica algoritmul Roy-Floyd. Cum la pasul i, determinăm drumurile minime între oricare două noduri folosind ca noduri intermediare elemente din mulţimea x₁, x₂, ..., x_i, putem răspunde la toate query-urile care au riscul asociat mai mic decât riscul nodului x_i, parcurgând în paralel query-urile şi nodurile. Astfel, complexitatea totală este O(N³+QlogQ).

Diagonala

O primă observaţie este aceea că dacă mutăm secvenţa de 1 de pe linia i cu i poziţii mai la stânga respectiv mai la dreapta, problema se reduce la aflarea celei mai lungi secvenţe verticale continue de 1.

Pentru a determina o astfel de secvenţă vom menţine două deque-uri, unul sortat descrescător pentru marginile din dreapta, iar celălalt crescător pentru marginile din stânga. În momentul în care introducem un nou interval, vom avea grijă să menţinem proprietăţile celor două deque-uri. Acum, există posibilitatea ca cel mai mare element din deque-ul pentru marginile din stânga să fie mai mare decât cel mai mic din deque-ul pentru marginile din dreapta, caz în care vom scoate pe rând elementele din cele două deque-uri până când cea mai mare margine din dreapta este mai mică sau egală cu cea mai mică margine din stânga. Astfel putem determina lungime maximă a unei coloane continue de 1 ce se termină pe linia actuală.