Solutii preONI 2006 - Runda a 2-a

(Categoria Competitii, autor(i) Echipa infoarena)

Runda a 2-a concursului preONI 2006 s-a incheiat. Acest articol va prezinta solutiile oficiale ale celor 7 probleme propuse.

Fiecare grupa a avut spre rezolvare 3 probleme, fiecare fiind catalogata de catre comisie ca fiind usoara, medie sau grea. Batalia pentru calificarea la finala este in toi!

Pentru mai multe detalii despre finala, cat si despre concursul preONI 2006 si sponsorii nostri va rugam sa consultati pagina preONI-2006.

Rezultatele finale sunt disponibile la:

Dificultatea problemelor nu a lasat nici de aceasta data de dorit. Desi ne-am fi asteptat la punctaje mai mari, rezultatele concurentilor au fost decente. Provocarile oferite de Infoarena sunt intr-adevar dificile, iar obtinerea unui punctaj apropiat de cel maxim nu este usor de realizat. In editiile ce vor urma vom tine cont de acest aspect. Pana atunci va invitam sa discutati despre aceasta runda de concurs pe forum-ul infoarena.

Ca de obicei, problemele din acest concurs au fost puse si in Arhiva de probleme, disponibile pentru rezolvare 24 de ore din 24. Va asteptam cu forte proaspete la runda a 3-a din 21 ianuarie 2006 !!!

Dame

(clasa a 9-a problema usoara)

In primul rand, numarul maxim de dame este N pentru N = 1 si N ≥ 4, si N-1 pentru N = 2, 3. Putem codifica solutia ca o permutare de la 1 la N, astfel asigurand ca nu exista doua dame pe aceeasi linie sau coloana. O solutie clasica care foloseste metoda backtracking si face verificarea daca o dama este atacata sau nu in O(1) va obtine 30 de puncte.
Verificarea in O(1) se face pastrand doi vectori pentru fiecare diagonala in functie de orientare, in care se marcheaza daca o diagonala este ocupata. O "imbunatatire" la backtracking este randomizarea ordinii in care se incearca completarea solutiei la fiecare pas. O astfel
de solutie merge usor si pentru N = 200 si ar fi obtinut cel putin 60 de puncte.
Exista mai multe metode prin care s-ar fi putut obtine 100 de puncte. O solutie greedy este urmatoarea: se incepe cu o solutie oarecare si cat timp exista doua dame care, daca s-ar interschimba coloanele lor, se imbunatateste solutia, se aplica interschimbarea. Daca
nu s-a obtinut o solutie buna, se reinitializeaza solutia initiala si se reaplica algoritmul. In practica, complexitatea algoritmului tinde la O(N log N), desi teoretic este O(N³). De asemenea pe masura ce N este mai mare, numarul necesar de reinitializari ale algoritmului tinde catre 0. Mai multe detalii gasiti aici
O alta solutie , matematica, se bazeaza pe un sablon de construire a solutiei in functie de restul lui N la 12.

Se insereaza numerele pare de la 2 la N intr-o lista
Daca restul lui N la 12 este 3 sau 9 se muta 2 la sfarsitul listei
Se insereaza numerele impare de la 1 la N in lista
Daca restul este 8 se interschimba perechile (3 1, 7 5, ...)
Daca restul este 2 se interschimba 1 cu 3 si 5 se muta la sfarsitul listei
Daca restul este 3 sau 9 se muta 1 si 3 la sfarsitul listei

Lista va codifica o solutie cum s-a precizat si inainte, al i-lea element reprezetand o dama pe randul i si pe coloana lista_i.
Aceasta solutie O(N) este preluata de aici

Zota & Chidil

(clasa a 9-a problema medie)

O solutie de complexitate O((M + N)lg N) este imediata. Se vor folosi doi vectori, fiecare continand coordonatele punctelor afectate de capcane, mai putin punctul de coordonate (0, 0), pentru a respecta conditia impusa in enunt. Primul vector vx va fi sortat dupa coordonata x, iar in caz de egalitate dupa coordonata y. Al doilea, vy, va fi sortat dupa y si, in caz de egalitate, dupa x.

La fiecare mutare executata de Chidil (un numar de pasi facut intr-o anume directie) se calculeaza numarul de celule afectate prin care trece. Pentru aceasta se vor aplica doua cautari binare in vectorul corespunzator.

Daca se deplaseaza inspre N sau S, cautarea se va face in vx, altel, in vy. Diferenta dintre cele doua valori returnate de cautarile binare furnizeaza numarul de celule afectate prin care Chidil trece la acea mutare.

Pentru un timp de executie bun, se recomanda folosirea functiei sort() din STL pentru sortare si a containerului pair<int, int> pentru pastrarea coordonatelor in cei doi vectori.

Grupuri

(clasa a 9-a problema grea, clasa a 10-a problema medie)

O limita superioara pentru numarul de grupuri este S / K unde S reprezinta suma canitatilor de animale. Este evident ca, daca putem construi X grupuri, putem construi si Y ≤ X grupuri, fapt care ne duce la ideea sa cautam binar numarul de grupuri. Pentru a verifica daca putem construi un numar de grupuri X ne imaginam completarea unei matrice cu X linii si K coloane, fiecare linie reprezetand un grup. Din restrictiile problemei elementele de pe fiecare linie trebuie sa fie distincte. Vom completa aceasta matrice coloana cu coloana, pentru fiecare cantitate de animale daca este ≤ X le punem pe toate in matrice, daca este > X punem doar X in matrice (deoarece daca punem mai multe vor fi cel putin doua pe aceeasi linie). Pentru primul exemplu din enunt, matricea se va completa astfel:

1 * * 1 2 * 1 2 3 1 2 3
1 * * 1 2 * 1 2 * 1 2 4
1 * * 1 * * 1 3 * 1 3 4
* * * 2 * * 2 3 * 2 3 4

Asadar , daca in final am putut completa toata matricea se pot forma X grupuri. Este evident ca strategia folosita de verificare este optima. Completarea matricei se face doar conceptual, verificarea avand complexitatea O(N) prin parcurgerea vectorului A, rezultand un algoritm de complexitate O(N lg(S/K)).Pe baza algoritmului descris mai sus, se poate obtine un algoritm O(N), desi acesta n-ar fi fost necesar pentru 100 de puncte.

Algoritmul lucreaza astfel: daca cel mai mare element este ≤ S/K , verificarea prezentata mai sus ne garanteaza ca vom putea obtine S/K grupuri, toate elementele fiind ≤ S/K se vor folosi toate S, iar matricea este (S/K)*K = S. Daca cel mai mare element este > S atunci putem rezolva aceeasi problema recursiv pentru cantitatile existente mai putin cea mai mare si grupuri de marime K-1. Acest rezultat va fi mai mic sau egal cu cel mai mare element, deci ne va ajunge pentru a completa grupurile la marimea K. Deoarece canitatile sunt date sortate, complexitatea este O(N).

1-2 perm

(clasa a 10-a problema usoara)

Problema a fost incadrata in categoria usoara deoarece la majoritatea problemelor de acest tip concurentii genereaza cu backtracking valorile pentru primele numere si deduc formula generala. In cazul acesta, formula se putea vedea destul de usor:

T[1] = 1, T[2] = 2, T[3] = 6, T[4] = 12;
T[i] = T[i - 1] + T[i - 3] + 2 * (i - 2)

Pentru cei mai curiosi din fire, vom demonstra cum se ajunge la aceasta formula. Fie A_i numarul permutarilor de lungime i care au 1 pe prima sau ultima pozitie, adica dublul numarului permutarilor care au 1 pe prima pozitie (exceptie face, ca in toti pasii care vor urma, permutarea de lungime 1). De asemenea, fie B_i numarul permutarilor de lungime i care nu au 1 pe prima sau ultima pozitie. Evident, T_i = A_i + B_i. Primele valori sunt

A[1] = 1, B[1] = 0
A[2] = 2, B[2] = 0
A[3] = 4, B[3] = 2
A[4] = 8, B[4] = 4

Pentru calculul lui A consideram urmatoarele cazuri:

incepem permutarea cu 1, 2 => avem A_i-1 posibilitati
incepem permutarea cu 1, 3, 2, 4 => avem A_i-3 posibilitati
incepem permutarea cu 1, 3 dar nu continuam cu 2 => vom mai avea o singura posibilitate, de forma (1, 3, 5, 7, 9, 8, 6, 4, 2). Adica ``urcam'' cu numerele impare si ``coboram'' cu cele pare pana la 2. Bineinteles, aceasta posibilitate poate fi considerata si in sens invers.
Deci A_i = A_i-1 + A_i-3 + 2.

Pentru calculul lui B incepem cu numarul 1 si observam ca celelalte numere pot fi completate doar alternativ (stanga-dreapta sau dreapta-stanga) pana la un anumit pas, si incepand de pe pozitia la care ne-am oprit, in unul din modurile calculate precedent. Pentru i = 7 incepand cu 1 avem cazurile:

(3, 1, 2) => in continuare A₅ moduri
(3, 1, 2, 4) => in continuare A₄ moduri
(5, 3, 1, 2, 4) => in continuare A₃ moduri
(5, 3, 1, 2, 4, 6) => in continuare A₂ moduri
(7, 5, 3, 1, 2, 4, 6) => in continuare A₁ moduri

Observam ca valorile calculate precedent in A sunt de fapt dublul celor de care avem noi nevoie, dar considerand si modul invers de completare alternativa, rezultatul obtinut va fi cel corect.
Deci B_i = A_i-2 + A_i-3 + ... + A₁, adica B_i = B_i-1 + A_i-2.

Am ajuns la urmatoarele 2 siruri recurente:

A_i = A_i-1 + A_i-3 + 2
B_i = B_i-1 + A_i-2

Mai facem urmatoarea observatie: A_i - B_i-1 = (A_i-1 + A_i-3 + 2) - (B_i-2 + A_i-3) = A_i-1 - B_i-2 + 2, ceea ce inseamna ca A_i - B_i-1 = 2 * (i - 1) (demonstratie prin inductie, tinand cont de faptul ca A₂ - B₁ = 2).

In sfarsit, sa calculam sirul T_i = A_i + B_i.
T_i = A_i + B_i = A_i-1 + A_i-3 + 2 + B_i-1 + A_i-2 = (A_i-1 + A_i-3) + (B_i-1 + B_i-3) + (A_i-2 - B_i-3) + 2 = T_i-1 + T_i-3 + (A_i-2 - B_i-3) + 2. Dupa cum am observat mai devreme A_i-2 - B_i-3 = 2 * (i - 3) => T_i = T_i-1 + T_i-3 + 2 * (i - 2), ceea ce ne propusesem sa demonstram.

Punctajele se obtin in modul urmator:

O(N²) timp, O(N) memorie ~ 50%
O(N) timp, O(N) memorie ~ 70%
O(N) timp, O(1) memorie ~ 90-100%

Desc

(clasa a 10-a problema grea, clasele 11-12 problema usoara)

O observatie evidenta ar fi faptul ca in cadrul produsului nu vor aparea decat divizorii lui N. De aceea vom creea vectorul dvz care contine toti cei D divizori ai lui N. In continuare se va construi matricea A, unde elementul A_i,j va retine numarul de posibilitati de a obtine divizorul i, folosind divizorii j, j+1, ..., D. Aceasta se va construi in ordine descrescatoare a coloanelor. Initial A_i,j= A_i,j+1 deoarce se vor folosi aceleasi moduri de descompunere folosind divizorii j+1, j+2, ..., D, apoi vom lua in considerare cazul in care se foloseste divizorul j. Pentru asta trebuie ca dvz_j sa divida pe dvz_i, iar in acest caz vom adauga la A_i,j pe A_X,j unde X este indicele divizoului dvz_i/dvz_j. Procesarea unei coloane trebuie sa se faca crescator deoarece X < i. Cautarea lui X se poate face fie binar, dar daca ne uitam mai atent vom observa ca valorile lui X sunt crescatoare deci putem continua cautarea liniar de la pasul la care ne oprisem pentru i-1. Acest lucru va asigura o complexitate totala O(D) pentru fiecare coloana a matricii. Complexitatea totala rezultand O(D²). Singura initializare care trebuie facuta va fi A_0,i = 1 pentru 1 ≤ i ≤ D deoarce se considera ca se poate obtine produsul 1 intr-un singur mod, iar rezultatul se va gasi in A_D,1.

Pentru a gasi cea de a K-a descompunere a lui N ne vom folosi de aceasta matrice. Incercam pe rand sa punem fiecare divizor pe prima pozitie. Cand punem divizorul i pe prima pozitie vom avea A_X,i posibilitati unde X reprezinta indicele divizorului N/dvz_i. Daca numarul acestor posibilitati este mai mic strict decat K se va scadea acest numar din K deoarece toate descompunerile care incep cu dvz_i sunt mai mici lexicografic decat varianta cautata de noi. Daca numarul acestor posibilitati este mai mare sau egal cu K atunci descompunerea cautata de noi incepe cu dvz_i si vom cauta in continuare a K-a descompunere pentru N/dvz_i folosind insa divizori mai mari decat dvz_i.

Struti

(clasele 11-12 problema medie)

Vom incerca sa rezolvam fiecare oferta in O(M*N), complexitatea finala a algoritmului fiind astfel O(P*M*N). Matricea de altitudini o vom nota cu mat. Intai vom determina maximul pe portiuni dreptunghiulare de forma [i,j]-[i+DX-1,j+DY-1], iar apoi, prin aceeasi metoda vom afla si minimul. Pentru a afla maximul pe astfel de portiuni, vom nota cu MAX_i,j = max{mat_i,j, mat_i+1,j ... mat_i+DX-1,j}. Pentru fiecare coloana, vom utiliza o stiva sortata crescator dupa linii si descrescator dupa valoare altitudinilor. Stiva va retine elemente situate pe pozitii intre i si i+DX-1, cu altitudinile sortate descrescator.

Daca avem stiva construita la linia i, atunci pentru linia urmatoare vom scoate primul element din stiva doar daca pozitia pe care se afla este mai mica sau egala cu i, iar elementul curent il vom introduce pentru a mentine stiva ordonata. Complexitatea acestui pas este O(M*N), pe fiecare coloana efectuandu-se O(M) operatii, pentru ca fiecare element este introdus si scos din stiva exact o data. Pentru a afla maximul intregii portiuni dreptunghiulare, aplicam acelasi procedeu, notand: MAX2_i,j = max{MAX_i,j, MAX_i,j+1 ... MAX_i,j+DY-1}.

Pentru a afla si minimul pe portiuni se procedeaza similar.

In plus, pentru o oferta vom procesa atat perechea (DX, DY), cat si (DY, DX), daca si numai daca DX diferit de DY. Altfel, vom procesa doar (DX, DY).

Camera

(clasele 11-12 problema grea)

Problema pare la prima vedere destul de complicata. O solutie posibila ar fi sa pornim cu poligonul initial si sa il intersectam cu cate o dreapta determinata de fiecare din laturile lui. Aceasta rezolvare ar putea parea destul de complicata pentru ca implica intersectii de drepte cu poligoane concave. Zona din care toate laturile poligonului sunt vizibile este cunoscuta sub numele de nucleu sau kernel in engleza. Pentru ca dintr-un punct sa fie vizibila o latura a poligonului, acest punct trebuie sa fie in semiplanul determinat de aceasta latura. De aici deducem ca nucleul poligonului este de fapt intersectia celor N semiplane determinate de laturile poligonului. Pornim la inceput cu o zona patrata care contine toate punctele poligonului, astfel ea va contine si nucleul poligonului. Vom taia pe rand cu semiplane acest patrat. Poligonul intermediar va fi tot timpul convex, ceea ce ne usureaza cu mult rezolvarea. Vedem in urmatoarea imagine un exemplu al pasilor algoritmului:

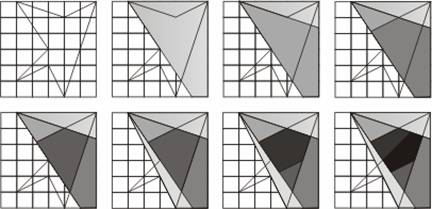
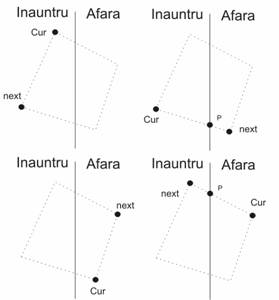
Parcurgem laturile poligonului intr-o ordine oarecare. Vom avea doi pointeri cur si next care vor reprezenta doua varfuri consecutive de pe poligonul care e solutia curenta. Daca ambele puncte sunt in interiorul semiplanului, atunci solutiei urmatoare ii adaugam punctul urmator. Daca punctul curent e in interior si punctul urmator este in exterior atunci solutiei ii adaugam punctul de intersectie p. Daca ambele puncte sunt in exterior procesam urmatoarea pereche. Daca punctul curent e in exterior si urmatorul punct este in interior atunci solutiei ii adaugam punctul de intersectie p si punctul urmator. Astfel obtinem un algoritm de complexitate O(n²). Mentionam ca acest algoritm poate fi folosit si la determinarea intersectiei a doua poligoane convexe.

infoarena informatica de performanta